Question

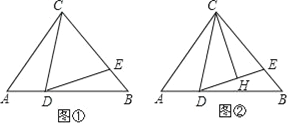
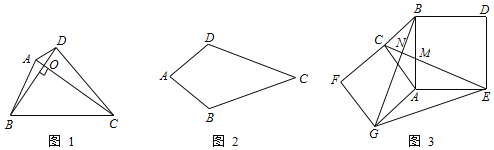
【题目】（1）问题发现：如图1，和均为等边三角形，点在的延长线上，连接，求证：．

（2）类比探究：如图2，和均为等腰直角三角形，，点在边的延长线上，连接．请判断：①的度数为_________．②线段之间的数量关系是_________．

（3）问题解决：在（2）中，如果，求线段的长．

Answer 1

【答案】（1）见解析；（2）①，②；（3）

【解析】

（1）根据等边三角形的性质得到AB=AC=BC，∠BAC=60°，AD=AE，∠DAE=60°，利用等量代换得∠BAD=∠CAE，则可根据“SAS”判断△ABD≌△ACE；

（2）根据等腰直角三角形的性质得到AB=AC，∠BAD=∠CAE，AD=AE，根据全等三角形的性质得到∠ACE=∠B=45°，BD=CE，等量代换即可得到结论；

（3）先证明△CDE是直角三角形，再计算BC=2，从而可得CE=3，再运用勾股定理可得DE的长.

（1）证明：和是等边三角形

，且

，即

在和中

（2）∵和均为等腰直角三角形，

∴AB=AC，∠BAC=∠DAE，AD=AE，

∴∠BAC+∠CAD=∠DAE+∠CAD，

∴∠BAD=∠CAE，

∴，

∴∠ACE=∠B=45°，BD=CE，

即BC+CD=CE，

故答案为：①；②

（3）由（2）知：

又，

，

在中，，

又，由（2）得

在中，

则线段的长是．