Question

如图，E、F是正方形ABCD的边AD上两个动点，满足AE=DF，连接CF交BD于G ,连接BE交AG于H．若正方形的边长为2

（1）求证：∠DAG=∠ABE

（2）若P是AB的中点，E在运动过程中，PH的值是否发生变化？若不变，请求出PH的值并说明理由．

（3）在（2）的条件下请求出DH的最小值．

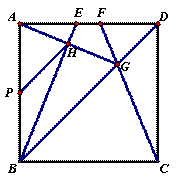
图一                    图二                      备用图

                                    

Answer 1

 (1)易证∵△AFG≌△DCG，∴∠DAG=∠DCG,

又易证 △ABE≌△DCF,  ∴∠DCG=∠ABE．

∴∠DAG=∠ABE．————————————————（3分）

        (2) ∵∠DAG=∠ABE, ∠DAG+∠BAH=90

∴∠ABE+∠BAH=90

∴∠AHB=90

又∵P是AB中点

∴PH是Rt△AHB斜边上中线

∴PH==1，是定值。————————————————（6分）

（3）∵PH==1，是定值

∴DH最小值就是当DH+PH最小的情况

∵两点之间线段最短

∴DH+PH最小为线段DP长

∴DH最小值为 ————————————————（9分）