题目内容
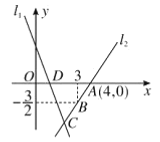
【题目】如图,直线![]() 的解析表达式为
的解析表达式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() .直线
.直线![]() 经过点
经过点![]() ,直线
,直线![]() 交于点
交于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的解析表达式;
的解析表达式;
(3)在![]() 轴上求作一点
轴上求作一点![]() ,使
,使![]() 的和最小,直接写出
的和最小,直接写出![]() 的坐标.
的坐标.
【答案】(1)D(1,0);(2)y=![]() x6;(3)
x6;(3)![]() (
(![]() ,0).
,0).
【解析】
(1)已知l1的解析式,令y=0求出x的值即可;
(2)设l2的解析式为y=kx+b,代入A、B坐标求出k,b的值即可;
(3)作点B关于x轴的对称点B’, 连接B’C交x轴于M,则点M即为所求,联立解析式可求出点C坐标,然后求出直线B’C的解析式,令y=0求出x的值即可.
解:(1)由y=3x+3,令y=0,得3x+3=0,
解得:x=1,
∴D(1,0);
(2)设直线l2的表达式为y=kx+b,
由图象知:A(4,0),B(3,![]() ),代入表达式y=kx+b,
),代入表达式y=kx+b,
得 ,解得:
,解得:
∴直线l2的解析表达式为y=![]() x6;
x6;
(3)作点B关于x轴的对称点B’,则B’的坐标的为(3,![]() ),连接B’C交x轴于M,则点M即为所求,
),连接B’C交x轴于M,则点M即为所求,
联立 ,解得:
,解得:![]() ,
,
∴C(2,-3),
设直线B’C的解析式为:y=mx+n,代入B’(3,![]() ),C(2,-3),
),C(2,-3),
得 ,解得:
,解得: ,
,
∴直线B’C的解析式为:y=![]() x12,
x12,
令y=0,即![]() x12=0,
x12=0,
解得:![]() ,
,
∴![]() 的坐标为(
的坐标为(![]() ,0).
,0).

 全能测控期末小状元系列答案
全能测控期末小状元系列答案【题目】中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表:
本数(本) | 人数(人数) | 百分比 |
5 | a | 0.2 |
6 | 18 | 0.36 |
7 | 14 | b |
8 | 8 | 0.16 |
合计 | c | 1 |
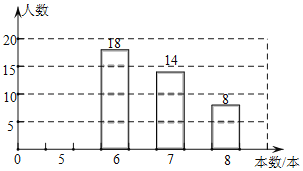
根据以上提供的信息,解答下列问题:
(1)a=_____,b=_____,c=______;
(2)补全上面的条形统计图;
(3)若该校八年级共有1200名学生,请你分析该校八年级学生课外阅读7本及以上的有多少名?
【题目】甲、乙两名队员参加设计训练,成绩分别被制成下列两个统计图:
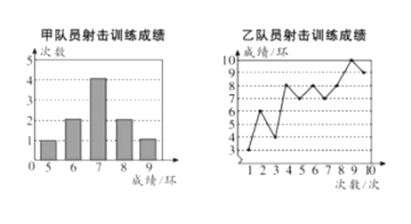
根据以上信息,整理分析数据如下:
平均数(环) | 中位数(环) | 众数(环) | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)表格中![]() ,
,![]() ,
,![]() ;
;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩,若选派其中一名参赛,你认为应选哪名队员?
(3)如果乙再射击![]() 次,命中
次,命中![]() 环,那么乙的射击成绩的方差 .(填“变大”“变小”或“不变”)
环,那么乙的射击成绩的方差 .(填“变大”“变小”或“不变”)