题目内容
8．
如图所示，在△ABC中，BD，CD分别是∠ABC和∠ACB的平分线，已知∠A=70°，求∠BDC的度数．
分析 根据角平分线的定义得到∠1=∠2，∠3=∠4，再根据三角形内角和定理得到∠1+∠3+∠BDC=180°，∠1+∠2+∠3+∠4+∠A=180°，利用等量代换得到2（180°-∠BDC）+∠A=180°，即有∠BDC=90°+$\frac{1}{2}$∠A．
解答 
解：如图，
∵∠ABC，∠ACB的平分线相交于点D，
∴∠1=∠2，∠3=∠4，
∵∠1+∠3+∠BDC=180°，∠1+∠2+∠3+∠4+∠A=180°，
∴2∠1+2∠3+∠A=180°，
∴2（180°-∠BDC）+∠A=180°，
∴∠BDC=90°+$\frac{1}{2}$∠A，
∵∠A=100°，
∴∠BDC=90°+$\frac{1}{2}$×70°=90°+35°=125°．
点评 本题考查了三角形内角和定理，熟知三角形内角和为180°是解答此题的关键．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
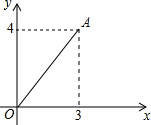如图，在直角坐标系中，线段OA的两个端点坐标分别为O（0，0），A（3，4），若把线段OA向右平移2个单位，得线段O′A′，则点O′的坐标为（2，0），点A′的坐标为（5，3）．
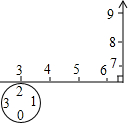如图所示，数轴被折成90°，圆的周长为4个单位长度，在圆的4等分点处标上数字0，1，2，3，先让圆周上数字2所对应的点与数轴上的数3所对应的点重合，数轴固定，圆紧贴数轴沿着数轴的正方向滚动，那么数轴上的数2013将与圆周上的数字0重合．
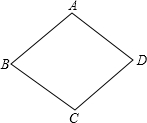如图，已知菱形ABCD，画一个矩形，使得A，B，C，D四点分别在矩形的四条边上，且矩形的面积为菱形ABCD面积的2倍．