题目内容
2.等腰三角形一个内角为100°,则其他角的度数为40°,40°.分析 根据100°角是钝角判断出只能是顶角,然后根据等腰三角形两底角相等解答.
解答 解:∵100°>90°,
∴100°的角是顶角,
∴$\frac{1}{2}$(180°-100°)=40°,
∴其他两角的度数分别为:40°,40°.
故答案为:40°,40°.
点评 本题考查了等腰三角形两底角相等的性质,先判断出100°的角是顶角是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13. 月球是地球的近邻,它的起源一直是人类不断探索的谜题之一.全球迄今进行了126次月球探测活动,因为研究月球可提高人类对宇宙的认识,包括认识太阳系的演化及特点,认识地球自然系统与太空自然现象之间的关系.我们已经认识到,在月球表面,白天阳光垂直照射的地方温度高达127℃,夜晚温度可降到-183℃.下面对“-183℃”的叙述不正确的是( )
月球是地球的近邻,它的起源一直是人类不断探索的谜题之一.全球迄今进行了126次月球探测活动,因为研究月球可提高人类对宇宙的认识,包括认识太阳系的演化及特点,认识地球自然系统与太空自然现象之间的关系.我们已经认识到,在月球表面,白天阳光垂直照射的地方温度高达127℃,夜晚温度可降到-183℃.下面对“-183℃”的叙述不正确的是( )
 月球是地球的近邻,它的起源一直是人类不断探索的谜题之一.全球迄今进行了126次月球探测活动,因为研究月球可提高人类对宇宙的认识,包括认识太阳系的演化及特点,认识地球自然系统与太空自然现象之间的关系.我们已经认识到,在月球表面,白天阳光垂直照射的地方温度高达127℃,夜晚温度可降到-183℃.下面对“-183℃”的叙述不正确的是( )
月球是地球的近邻,它的起源一直是人类不断探索的谜题之一.全球迄今进行了126次月球探测活动,因为研究月球可提高人类对宇宙的认识,包括认识太阳系的演化及特点,认识地球自然系统与太空自然现象之间的关系.我们已经认识到,在月球表面,白天阳光垂直照射的地方温度高达127℃,夜晚温度可降到-183℃.下面对“-183℃”的叙述不正确的是( )| A. | -183是一个负数 | B. | -183表示在海平面以下183米 | ||
| C. | -183在数轴上的位置在原点的左边 | D. | -183是一个比-100小的数 |
10.(-$\frac{2}{3}$)2012×1.52013×(-1)2014=( )
| A. | -1.5 | B. | $-\frac{2}{3}$ | C. | 1.5 | D. | -1 |
11.关于x的二次函数y=x2+2kx+k-1,下列说法正确的是( )
| A. | 对任意实数k,函数与x轴都没有交点 | |
| B. | 存在实数n,满足当x≥n时,函数y的值都随x的增大而减小 | |
| C. | 不存在实数n,满足当x≤n时,函数y的值都随x的增大而减小 | |
| D. | 对任意实数k,抛物线y=x2+2kx+k-1都必定经过唯一定点 |
12.$\sqrt{2}$的相反数的绝对值是( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -$\sqrt{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
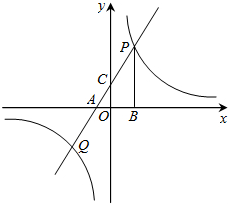 如图,经过点A(-2,0)的一次函数y=ax+b(a≠0)与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于P、Q两点,过点P作PB⊥x轴于点B.已知tan∠PAB=$\frac{3}{2}$,点B的坐标为(4,0).
如图,经过点A(-2,0)的一次函数y=ax+b(a≠0)与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于P、Q两点,过点P作PB⊥x轴于点B.已知tan∠PAB=$\frac{3}{2}$,点B的坐标为(4,0).