题目内容
在直角△ABC中,∠C=90°,a、b、c为∠A、∠B、∠C所对应的边长,那么下列关系中,正确的是
- A.c=a•sinA
- B.
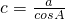
- C.

- D.c=a•tanA
C
分析:根据三角函数定义:(1)正弦:我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA.
(2)余弦:锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA.
(3)正切:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA.
分别进行分析即可.
解答: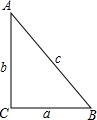 解:A、∵
解:A、∵ =sinA,∴c=
=sinA,∴c= ,故此选项错误;
,故此选项错误;
B、∵ =cosA,∴c=
=cosA,∴c=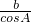 ,故此选项错误;
,故此选项错误;
C、∵ =sinA,∴c=
=sinA,∴c= ,故此选项正确;
,故此选项正确;
D、∵ =tanA,∴a=b•tanA,故此选项错误;
=tanA,∴a=b•tanA,故此选项错误;
故选:C.
点评:此题主要考查了锐角三角函数的定义,关键是熟练掌握锐角三角函数的定义.
分析:根据三角函数定义:(1)正弦:我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA.
(2)余弦:锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA.
(3)正切:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA.
分别进行分析即可.
解答:
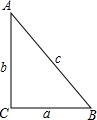 解:A、∵
解:A、∵ =sinA,∴c=
=sinA,∴c= ,故此选项错误;
,故此选项错误;B、∵
 =cosA,∴c=
=cosA,∴c=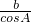 ,故此选项错误;
,故此选项错误;C、∵
 =sinA,∴c=
=sinA,∴c= ,故此选项正确;
,故此选项正确;D、∵
 =tanA,∴a=b•tanA,故此选项错误;
=tanA,∴a=b•tanA,故此选项错误;故选:C.
点评:此题主要考查了锐角三角函数的定义,关键是熟练掌握锐角三角函数的定义.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 如图,在直角△ABC中,∠C=90°,若AB=5,AC=4,则tan∠B=( )
如图,在直角△ABC中,∠C=90°,若AB=5,AC=4,则tan∠B=( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在直角△ABC中,∠C=90°,BD平分∠ABC且交AC于D,若AP平分∠BAC交BD于P,求∠APB的度数.
如图,在直角△ABC中,∠C=90°,BD平分∠ABC且交AC于D,若AP平分∠BAC交BD于P,求∠APB的度数. 已知:如图,在直角△ABC中,AD=DE=EB,且CD2+CE2=1,则斜边AB的长为
已知:如图,在直角△ABC中,AD=DE=EB,且CD2+CE2=1,则斜边AB的长为 如图,在直角△ABC中,∠C=90°,AB的垂直平分线交AB于D,交AC于F,且BE平分∠ABC,则∠A=( )
如图,在直角△ABC中,∠C=90°,AB的垂直平分线交AB于D,交AC于F,且BE平分∠ABC,则∠A=( ) 如图,在直角△ABC中,∠A=90°,BC边上的垂直平分线交AC于点D;BD平分∠ABC,已知AC=m+2n,BC=2m+2n,则△BDE的周长为
如图,在直角△ABC中,∠A=90°,BC边上的垂直平分线交AC于点D;BD平分∠ABC,已知AC=m+2n,BC=2m+2n,则△BDE的周长为