题目内容
三角形ABC中,G是BC上一点,D,E分别在边AB,AC上,DE∥BC,M为直线DE上一点,N为直线GD上一点,∠DMN=∠B
(1)如图a,当点M在DE上,点N在DG上时,求证:∠BDN=∠MND;
(2)当点M在ED延长线上,点N在GD延长线上时,请在图b中画出图形,此时∠BDN与∠MND的数量关系是
(3)在(2)的条件下,延长DG交AC延长线于点F,若∠A=60°,∠MND=75°,求∠F的度数.

(1)如图a,当点M在DE上,点N在DG上时,求证:∠BDN=∠MND;
(2)当点M在ED延长线上,点N在GD延长线上时,请在图b中画出图形,此时∠BDN与∠MND的数量关系是
∠BDN+∠MND=180°
∠BDN+∠MND=180°
;(3)在(2)的条件下,延长DG交AC延长线于点F,若∠A=60°,∠MND=75°,求∠F的度数.

分析:(1)利用平行线的性质得出∠B=∠ADE,进而得出AB∥MN,即可得出答案;
(2)利用(1)中解题思路,首先判断AB∥MN,进而利用平行线的性质得出;
(3)利用(2)所求得出∠MND=∠ADN=75°,进而利用三角形的外角得出即可.
(2)利用(1)中解题思路,首先判断AB∥MN,进而利用平行线的性质得出;
(3)利用(2)所求得出∠MND=∠ADN=75°,进而利用三角形的外角得出即可.
解答: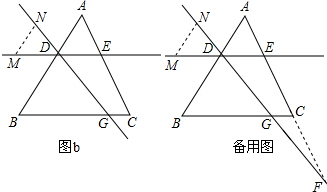 (1)证明:∵DE∥BC,
(1)证明:∵DE∥BC,
∴∠B=∠ADE,
∵∠DMN=∠B,
∴∠ADE=∠DMN,
∴AB∥MN,
∴∠BDN=∠MND;
(2)解:∵DE∥BC,
∴∠B=∠ADE,
∵∠DMN=∠B,
∴∠ADE=∠DMN,
∴AB∥MN,
∴∠BDN+∠MND=180°,
故答案为:∠BDN+∠MND=180°;
(3)解:由(2)得:∵AB∥MN,
∴∠MND=∠ADN=75°,
∵∠A+∠F=∠ADN=75°,∠A=60°,
∴∠F=15°.
 (1)证明:∵DE∥BC,
(1)证明:∵DE∥BC,∴∠B=∠ADE,
∵∠DMN=∠B,
∴∠ADE=∠DMN,
∴AB∥MN,
∴∠BDN=∠MND;
(2)解:∵DE∥BC,
∴∠B=∠ADE,
∵∠DMN=∠B,
∴∠ADE=∠DMN,
∴AB∥MN,
∴∠BDN+∠MND=180°,
故答案为:∠BDN+∠MND=180°;
(3)解:由(2)得:∵AB∥MN,
∴∠MND=∠ADN=75°,
∵∠A+∠F=∠ADN=75°,∠A=60°,
∴∠F=15°.
点评:此题主要考查了平行线的性质以及三角形的外角等知识,根据已知得出AB∥MN是解题关键.

练习册系列答案
相关题目
 如图,三角形ABC中,AD是BC边上的中线,其中,AC=17,BC=30,AD=8,请说明AB=AC.
如图,三角形ABC中,AD是BC边上的中线,其中,AC=17,BC=30,AD=8,请说明AB=AC.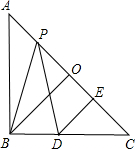 且PB=PD,DE⊥AC,垂足为点E.求证:
且PB=PD,DE⊥AC,垂足为点E.求证: 如图所示,在等边三角形ABC中,O是三个内角平分线的交点,OD∥AB,OE∥AC,则图中等腰三角形的个数是( )
如图所示,在等边三角形ABC中,O是三个内角平分线的交点,OD∥AB,OE∥AC,则图中等腰三角形的个数是( )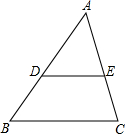 如图,在三角形ABC中,D是AB边上一点,E是AC边上一点,∠ADE=60°,∠AED=40°,∠B=60°.
如图,在三角形ABC中,D是AB边上一点,E是AC边上一点,∠ADE=60°,∠AED=40°,∠B=60°.