题目内容
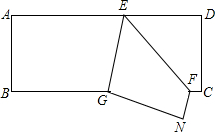 如图所示,把一张长方形纸片ABCD沿EF折叠,若∠EFC=130°,求∠DEG的度.
如图所示,把一张长方形纸片ABCD沿EF折叠,若∠EFC=130°,求∠DEG的度.考点:平行线的性质,翻折变换(折叠问题)
专题:
分析:由平行线的性质可求得∠DEF,由折叠的性质可得∠GEF=∠DEF,可求得∠DEG.
解答:解:
∵AD∥BC,
∴∠DEF+∠EFC=180°,
∴∠DEF=180°-∠EFC=180°-130°=50°,
又由折叠的性质可得∠GEF=∠DEF=50°,
∴∠DEG=100°.
∵AD∥BC,
∴∠DEF+∠EFC=180°,
∴∠DEF=180°-∠EFC=180°-130°=50°,
又由折叠的性质可得∠GEF=∠DEF=50°,
∴∠DEG=100°.
点评:本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.

练习册系列答案
相关题目
甲做180个机器零件比乙做240个机器零件所用的时间少
h,已知两人每小时共做70个零件,求甲、乙每小时做多少个零件?若设甲每小时做x个零件,下列方程正确的是( )
| 2 |
| 3 |
A、
| ||||||
B、
|
 如图,已知AC∥DE,∠1=∠2,∠B=∠3,试说明AD∥BC的理由.
如图,已知AC∥DE,∠1=∠2,∠B=∠3,试说明AD∥BC的理由. 如图,三点A,B,D在数轴上,点A,B在数轴上表示问数分别为-12,16(设定:数轴上A,B之间的距离记为AB)
如图,三点A,B,D在数轴上,点A,B在数轴上表示问数分别为-12,16(设定:数轴上A,B之间的距离记为AB)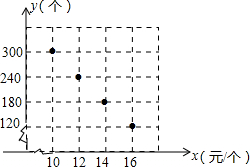 某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.这种许愿瓶的进价为6元/个,根据市场调查,一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:
某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.这种许愿瓶的进价为6元/个,根据市场调查,一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示: