题目内容
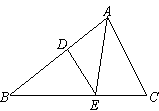
如图所示，G为△ABC重心（即AD，BE，CF分别为各边的中线），若已知S△EFG=1，则S△ABC为
- A.2
- B.4
- C.8
- D.12
D
分析：先根据EF∥BC1求出△EFG∽△BCG，再根据相似三角形的性质求出S△BCG的值，再根据三角形重心的性质即可解答．
解答：∵AD，BE，CF分别为各边的中线，
∴EF∥BC，△EFG∽△BCG，EF=
BC，
∴S△BCG=4S△EFG=4，
又∵G为△ABC重心，∴AG=2GD，
∴S△ABG+S△ACG=2S△BCG=8，
∴S△ABC=12．
故选D．
点评：此题要熟悉三角形的重心的性质．掌握比较两个三角形的面积的两种方法：利用相似或利用面积公式．
分析：先根据EF∥BC1求出△EFG∽△BCG，再根据相似三角形的性质求出S△BCG的值，再根据三角形重心的性质即可解答．
解答：∵AD，BE，CF分别为各边的中线，
∴EF∥BC，△EFG∽△BCG，EF=
BC，∴S△BCG=4S△EFG=4，
又∵G为△ABC重心，∴AG=2GD，
∴S△ABG+S△ACG=2S△BCG=8，
∴S△ABC=12．
故选D．
点评：此题要熟悉三角形的重心的性质．掌握比较两个三角形的面积的两种方法：利用相似或利用面积公式．
练习册系列答案
发散思维新课堂系列答案
相关题目
2、如图所示，D为AB边上一点，AD：DB=3：4，DE∥AC交BC于点E，则S△BDE：S△AEC等于（ ）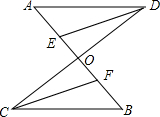
已知如图所示，O为AB、CD的中点，AE=BF，你从图中可以找到全等三角形共（ ）
