题目内容
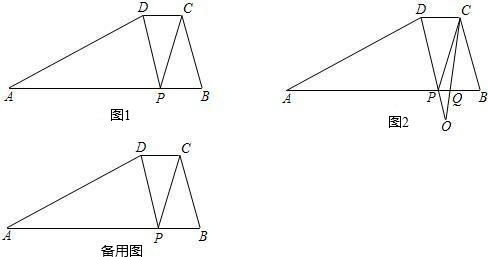
已知在梯形ABCD中,AD∥BC,AD<BC,且BC=6,AB=DC=4,点E是AB的中点,点P是BC边上一点.
(1)当BP=2时.求证:△BEP∽△CPD;
(2)若BP=5,过点P作射线PF,交CD所在的直线于点F,使得△BEP与△CPF相似.求此时CF的长度.
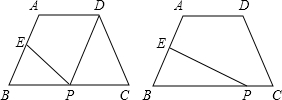
(1)证明:∵在梯形ABCD中,AD∥BC,AB=DC,
∴∠B=∠C.
∵BE=2,BP=2,CP=4,CD=4,
∴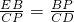 ,
,
∴△BEP∽△CPD.
(2)解:由已知,BP=5,BE=2,CP=1,
由(1)∠B=∠C,
若要△BEP与△CPF相似,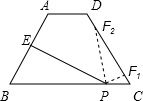
则只需∠BPE=∠CPF或∠BPE=∠CFP即可.
①当∠BPE=∠CPF时(点F落在图中F1处),△BPE∽△CPF
此时,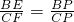 ,可得CF=
,可得CF=
②当∠BPE=∠CFP时(点F落在图中F2处),△BPE∽△CFP
此时,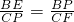 ,可得CF=
,可得CF=
∴当△BEP与△CPF相似时,CF的长度为 或
或 .
.
分析:(1)根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定;
(2)若要△BEP与△CPF相似,则只需∠BPE=∠CPF或∠BPE=∠CFP即可,那么分两种情况进行考虑.
点评:主要考查对相似三角形的判定的理解及运用,难易程度适中.
∴∠B=∠C.
∵BE=2,BP=2,CP=4,CD=4,
∴
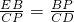 ,
,∴△BEP∽△CPD.
(2)解:由已知,BP=5,BE=2,CP=1,
由(1)∠B=∠C,
若要△BEP与△CPF相似,

则只需∠BPE=∠CPF或∠BPE=∠CFP即可.
①当∠BPE=∠CPF时(点F落在图中F1处),△BPE∽△CPF
此时,
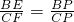 ,可得CF=
,可得CF=
②当∠BPE=∠CFP时(点F落在图中F2处),△BPE∽△CFP
此时,
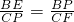 ,可得CF=
,可得CF=
∴当△BEP与△CPF相似时,CF的长度为
 或
或 .
.分析:(1)根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定;
(2)若要△BEP与△CPF相似,则只需∠BPE=∠CPF或∠BPE=∠CFP即可,那么分两种情况进行考虑.
点评:主要考查对相似三角形的判定的理解及运用,难易程度适中.

练习册系列答案
相关题目
 9、如图,已知在梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G.
9、如图,已知在梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G. ;
;