Question

已知某二次函数图象的顶点坐标是(－1，2)，且过点(0，)．

(1)求此二次函数的关系式，并在下图中画出它的图象；

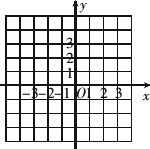
(2)求证：对于任意实数m，点M(m，－m²)都不在这个二次函数的图象上．

Answer 1

答案：
解析：

分析：(1)题中给出了二次函数图象的顶点坐标(1，2)，所以可设其函数关系式为y＝a(x＋1)2＋2，将点(0，)代入求出a的值即可；(2)将点M的坐标代入函数关系式中，看所得方程是否有解． 　　解：(1)由于二次函数图象的顶点坐标是(－1，2)，所以可设此二次函数的关系式为y＝a(x＋1)2＋2． 　　因为点(0，)在它的图象上，所以有＝a(0＋1)2＋2．解得a＝－． 　　所以，所求二次函数的关系式为y＝－(x＋1)2＋2，其图象如图所示． 　　(2)证明：假设点M在此二次函数的图象上，则－m2＝－(m＋1)2＋2．整理，得m2－2m＋3＝0． 　　因为b2－4ac＝(－2)2－4×1×3＝－8＜0，所以方程无解，即假设不成立． 　　所以，对于任意实数m，点M(m，－m2)都不在这个二次函数的图象上．