题目内容
 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则下列结论一定正确的是( )
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则下列结论一定正确的是( )| A、∠1+∠2=360°-2(∠B+∠C) | ||
| B、∠1+∠2=180°-2(∠B+∠C) | ||
| C、∠1+∠2=180°-(∠B+∠C) | ||
D、∠1+∠2=360°-
|
分析:根据四边形的内角和是360°和平角的定义求解.
解答: 解:因为∠A+∠A+∠AEA′+∠ADA′=360°
解:因为∠A+∠A+∠AEA′+∠ADA′=360°
又因为∠1+∠AEA′+∠2+∠ADA′=360°,
所以∠A+∠A′=∠1+∠2,
又因为∠A=∠A′,
所以2∠A′=∠1+∠2,即∠1+∠2=360°-2(∠B+∠C).
故选A.
 解:因为∠A+∠A+∠AEA′+∠ADA′=360°
解:因为∠A+∠A+∠AEA′+∠ADA′=360°又因为∠1+∠AEA′+∠2+∠ADA′=360°,
所以∠A+∠A′=∠1+∠2,
又因为∠A=∠A′,
所以2∠A′=∠1+∠2,即∠1+∠2=360°-2(∠B+∠C).
故选A.
点评:本题考查三角形的内角和定理,图形在折叠的过程,会出现全等的图形--相等的线段、相等的角,是隐含的条件,注意运用.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
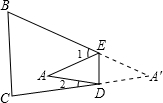 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,

 20、如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,∠A与∠1、∠2之间存在一种始终保持不变的数量关系,这个数量关系是
20、如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,∠A与∠1、∠2之间存在一种始终保持不变的数量关系,这个数量关系是 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,