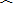题目内容

如图，把Rt△ABC依次绕顶点沿水平线翻转两次，若∠C=90°，AC=
3
，BC=1，那么AC边从开始到结束所扫过的图形的面积为（　　）
A．
7π
4
B．
7π
12
C．
9π
4
D．
25π
12

由勾股定理得：AB=
AC2+BC2
=
(
3
)2+12
=2，
第一次翻转是以点C为圆心，AC为半径，圆心角为90°的扇形，
S1=
nπR2
360
=
90×π×(
3
)2
360
=
3π
4
；
第二次翻转是以点B为圆心，以AB、BC为半径，圆心角为120°的圆环面积，
面积S2=
120×π×22
360
-
120π×12
360
=π；
故AC边从开始到结束所扫过的图形的面积为S=
3π
4
+π=
7
4
π．
故选A．
练习册系列答案
相关题目
如图所示，等边三角形ABC的边长为a，分别以点A，B，C为圆心，以
a
2
为半径的圆两两相切于点D，E，F，求
DE
，
EF
，
FD
围成的图形面积S（图中阴影部分）．
如图，图中的两条弧属于同心圆，若OA=1，OD=
5
，有一条也属于此同心圆的弧PQ能平分阴影部分的面积，那么OQ=______；请你将图中的阴影部分分为面积相等但不全等的两部分，简要说明作法（不要求证明）______．
如图，圆心角都是90°的扇形OAB与扇形OCD叠放在一起，连接AC，BD．
（1）求证：△AOC≌△BOD；
（2）若OA=3cm，OC=1cm，求阴影部分的面积．
如图，AB、CD为⊙O的四点，
AB
+
CD
=
AC
+
BD
，AB=8，DC=4，图中阴影部分的面积和为______．
如图，AB是⊙O的直径，弦CD⊥AB，∠CDB=30°，CD=2
3
，则阴影部分图形的面积为（　　）
A．4πB．2πC．πD．
2π
3
如图，菱形OABC中，∠A=120°，OA=1，将菱形OABC绕点O按顺时针方向旋转90°，则图中由弧BB′，B′A′，弧A′C，CB围成的阴影部分的面积是______．（结果保留根号）
如图，圆心角都是90°的扇形OAB与扇形OCD叠放在一起，连接AC，BD．
（1）求证：AC=BD；
（2）若图中阴影部分的面积是
3
4
πcm2，OA=2cm，求OC的长．
扇形OAB的半径OA=1，圆心角∠AOB=90°，点C是弧AB上的动点，连结AC和BC，记弦AC、CB与弧AC、CB围成的阴影部分的面积为S，则S的最小值为（　　）
A．
π
4
-
1
2
B．
π
4
-
2
2
C．
π
4
-
3
4
-
1
4
D．
π
8
-
1
4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网