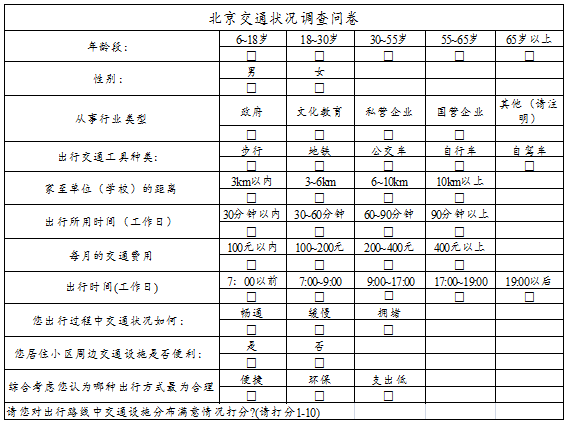
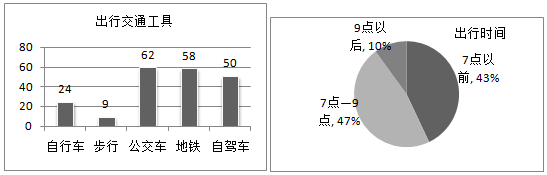
题目内容
8．在△ABC中，若∠A=60°，∠B：∠C=2：1，则∠B=80°．分析 先根据三角形内角和定理，求得∠B+∠C=120°，再根据∵∠B：∠C=2：1，求得∠B=80°，∠C=40°即可．
解答 解：∵∠A=60°，
∴∠B+∠C=120°，
又∵∠B：∠C=2：1，
∴∠B=80°，∠C=40°．
故答案为：80°．
点评 本题主要考查了三角形内角和定理的运用，解题时注意三角形内角和等于180°．
练习册系列答案
阅读快车系列答案
相关题目
实验数据显示，一般成人喝半斤低度白酒后，1.5小时内其血液中酒精含量y（毫克/百毫升）与时间x（时）的关系可近似地用二次函数y=-200x2+400x刻画；1.5小时后（包括1.5小时）y与x可近似地用反比例函数y=$\frac{k}{x}$（k＞0）刻画（如图所示）．
16．
如图，把一个长方形纸片沿EF折叠后，点D，C分别落在D'，C'的位置．若∠EFC'=115°，则∠AED'等于（ ）
如图，把一个长方形纸片沿EF折叠后，点D，C分别落在D'，C'的位置．若∠EFC'=115°，则∠AED'等于（ ）| A． | 70° | B． | 65° | C． | 50° | D． | 25° |
20．
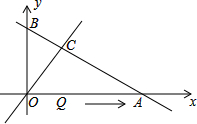如图，直线y=-$\frac{1}{2}$x+3与坐标轴分别交于A，B两点，与直线y=x交于点C，线段OA上的点Q以每秒1个单位长度的速度从点O出发向点A作匀速运动，运动时间为t秒，连接CQ．若△OQC是等腰直角三角形，则t的值为 （ ）
如图，直线y=-$\frac{1}{2}$x+3与坐标轴分别交于A，B两点，与直线y=x交于点C，线段OA上的点Q以每秒1个单位长度的速度从点O出发向点A作匀速运动，运动时间为t秒，连接CQ．若△OQC是等腰直角三角形，则t的值为 （ ）| A． | 2 | B． | 4 | C． | 2或3 | D． | 2或4 |
17．下列计算正确的是（ ）
| A． | a2+a2=2a4 | B． | 5y-3y=2 | C． | 3x2y-2yx2=x2y | D． | 3a+2b=5ab |