题目内容
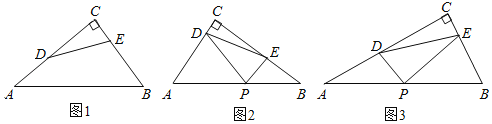
【题目】如图,四边形![]() 内一点
内一点![]() 满足
满足![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
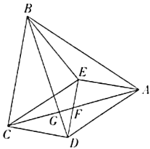
(1)![]() 的度数为__________.
的度数为__________.
(2)若四边形![]() 是平行四边形
是平行四边形
①求证:![]() ;
;
②若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)①证明见解析;②4
;(2)①证明见解析;②4
【解析】
(1)根据等式的性质求得∠BED=∠CEA,然后利用SAS定理求得△BED≌△CEA,从而得到∠BDE=∠CAE,然后求得∠AFE+∠EAF=90°,问题得解;
(2)①结合平行四边形和等腰直角三角形的性质求得![]() ,根据周角360°求得
,根据周角360°求得![]() ,然后利用边角边定理求得
,然后利用边角边定理求得![]() ,
,![]() ,从而得到
,从而得到![]() ,
,![]() ,问题得解;
,问题得解;
②由①求得![]() ,从而得到
,从而得到![]() ,从而求得
,从而求得![]() ,用AA定理证明
,用AA定理证明![]() ,然后根据相似三角形的性质列比例式求解.
,然后根据相似三角形的性质列比例式求解.
解:(1)∵![]()
∴![]()
∴∠BED=∠CEA
又∵![]() ,
,![]() ,
,
∴△BED≌△CEA
∴∠BDE=∠CAE
又∵∠CFD=∠AFE,∠AFE+∠EAF=90°
∴∠BDE+∠AFE=90°
即![]()
故答案为:90°
(2)①∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ;
;
∵![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
②∵![]() ,
,![]()
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.

 天天向上口算本系列答案
天天向上口算本系列答案【题目】某中学初三年级积极推进走班制教学.为了了解一段时间以来,“至善班”的学习效 果,年级组织了多次定时测试,现随机选取甲、乙两个“至善班”,从中各抽取![]() 名同学在某一次定时测试中的数学成绩,其结果记录如下:
名同学在某一次定时测试中的数学成绩,其结果记录如下:
收集数据:
“至善班”甲班![]() 的名同学的数学成绩统计(满分为 100 分)(单位:分)
的名同学的数学成绩统计(满分为 100 分)(单位:分)
![]()
![]()
“至善班”乙班的![]() 名同学的数学成绩统计(满分为 100 分)(单位:分)
名同学的数学成绩统计(满分为 100 分)(单位:分)
![]()
![]()
整理数据:(成绩得分用![]() 表示)
表示)
分数 数量 班级 |
|
|
|
|
|
甲班(人数) | 1 | 3 | 4 | 6 | 6 |
乙班(人数) | 1 | 1 | 8 | 6 | 4 |
分析数据,并回答下列问题:
![]() 完成下表:
完成下表:
平均数 | 中位数 | 众数 | |
甲班 |
|
|
|
乙班 |
|
|
|
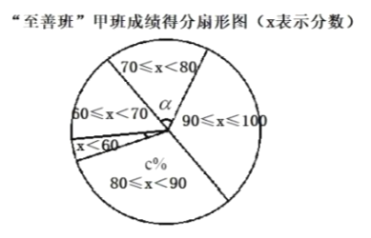
![]() 在“至善班”甲班的扇形图中, 成绩在
在“至善班”甲班的扇形图中, 成绩在![]() 的扇形中,所对的圆心角
的扇形中,所对的圆心角![]() 的度数为 . 估计全部“至善班”的
的度数为 . 估计全部“至善班”的![]() 人中优秀人数为 人.(
人中优秀人数为 人.(![]() 分及以上为优秀).
分及以上为优秀).
![]() 根据以上数据,你认为“至善班” 班(填“甲”或“乙”)所选取做样本 的同学的学习效果更好一些,你所做判断的理由是:
根据以上数据,你认为“至善班” 班(填“甲”或“乙”)所选取做样本 的同学的学习效果更好一些,你所做判断的理由是:
①
②
【题目】调查作业:了解你所住小区家庭3月份用气量情况.
小天、小东和小芸三位同学住在同一小区,该小区共有300户家庭,每户家庭人数在2—5之间,这300户家庭的平均人数约为3.3.
小天、小东和小芸各自对该小区家庭3月份用气量情况进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2、表3,
表1抽样调查小区4户家庭3月份用气量统计表(单位:![]() )
)
家庭人数 | 2 | 3 | 4 | 5 |
用气量 | 14 | 19 | 21 | 26 |
表2抽样调查小区15户家庭3月份用气量统计表(单位:![]() )
)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
用气量 | 10 | 11 | 15 | 13 | 14 | 15 | 17 | 17 | 18 | 18 | 18 | 18 | 18 | 20 | 22 |
表3抽样调查小区15户家庭3月份用气量统计表(单位:![]() )
)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
用气量 | 10 | 12 | 13 | 14 | 17 | 17 | 18 | 20 | 20 | 21 | 22 | 26 | 31 | 28 | 31 |
根据以上材料回答问题:
(1)小天、小东和小芸三人中,哪一位同学抽样调查的数据能较好地反应出该小区家庭3月份用气量情况?请简要说明其他两位同学抽样调查的不足之处;
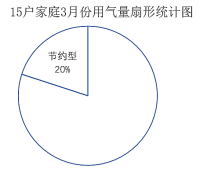
(2)小东将表2中的数据按用气量![]() 大小分为三类;
大小分为三类;
①节约型:![]() ;
;
②居中型:![]() ;
;
③偏高型:![]() ;并绘制成如下扇形统计图,请帮助他将扇形图补充完整;
;并绘制成如下扇形统计图,请帮助他将扇形图补充完整;
(3)小芸算出表3中3月份平均每人的用量为![]() ,请估计该小区3月份的总用气量.
,请估计该小区3月份的总用气量.