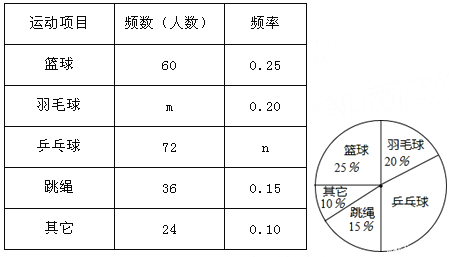
��Ŀ����
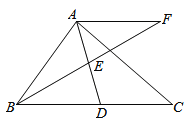
����Ŀ����ͼ��A��-4��![]() ��,B��-1��2����һ�κ���y=kx+b��ͼ���뷴��������
��,B��-1��2����һ�κ���y=kx+b��ͼ���뷴��������![]() ��m��0��m��0���ĺ���ͼ����������㣬AC��x���ڵ�C��BD��y���ڵ�D
��m��0��m��0���ĺ���ͼ����������㣬AC��x���ڵ�C��BD��y���ڵ�D
��1�����ݺ���ͼ��ֱ�ӻش����⣺�ڵڶ������ڣ���xȡ��ֵʱ��һ�κ�����ֵ���ڷ�����������ֵ��
��2����һ�κ����ı���ʽ��m��ֵ��
��3����P���߶�AB��һ�㣬����PC,PD,����PCA����PBD�������ȣ����P�����ꡣ
���𰸡���1��-4��x��-1����2��y=![]() x+
x+![]() ��-2����3����-
��-2����3����-![]() ��
��![]() ����
����
��������
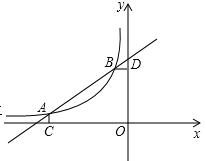
�����������1������һ�κ���ͼ�����Ϸ��IJ����Dz���ʽ�Ľ⣬�۲�ͼ�ɵô𰸣�
��2�����ݴ���ϵ�������ɵú�������ʽ��
��3�����������������ȣ��ɵô𰸣�
�����������1����ͼ���һ�κ���ͼ�����ϵIJ��֣�-4��x��-1��
��-4��x��-1ʱ��һ�κ������ڷ�����������ֵ��
��2����һ�κ����Ľ���ʽΪy=kx+b��
y=kx+b��ͼ����㣨-4��![]() ������-1��2������
������-1��2������
 ��
��
���![]()
һ�κ����Ľ���ʽΪy=![]() x+
x+![]() ��
��
����������y=![]() ͼ����㣨-1��2����
ͼ����㣨-1��2����
m=-1��2=-2��
��3������PC��PD����ͼ��

��P��x��![]() x+
x+![]() ��
��
����PCA����PDB�����ȵ�
![]() ��
��![]() ����x+4��=
����x+4��=![]() ��|-1|����2-
��|-1|����2-![]() x-
x-![]() ����
����
x=-![]() ��y=
��y=![]() x+
x+![]() =
=![]() ��
��
��P�������ǣ�-![]() ��
��![]() ����
����

 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�