题目内容
如图,在平面直角坐标系中,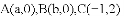
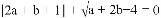 .
.
(1)求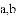
(2)①在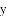
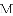
 ,求点
,求点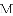
②在坐标轴上一共存在多少个点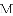
 成立?请直接写出符合条件的点
成立?请直接写出符合条件的点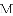

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
题目内容
如图,在平面直角坐标系中,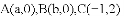
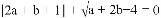 .
.
(1)求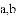
(2)①在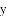
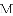
 ,求点
,求点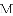
②在坐标轴上一共存在多少个点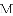
 成立?请直接写出符合条件的点
成立?请直接写出符合条件的点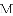

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案