题目内容
18.已知反比例函数y=$\frac{-k}{x}$(k≠0)的图象上有点A(1,-k)和B(-1,k),点C(-$\frac{1}{2}$,n+1)在直线y=k(x+$\frac{7}{4}$)上,且△ABC是以AB为斜边的直角三角形.(1)用n的代数式表示k;
(2)求反比例函数的函数表达式.
分析 (1)把点C(-$\frac{1}{2}$,n+1)代入y=k(x+$\frac{7}{4}$)利用待定系数法即可求得;
(2)作CN∥y轴,交过B作y轴的垂线于N,过A作AM⊥CN于M,根据点的坐标表示出AM=$\frac{3}{2}$,BN=$\frac{1}{2}$,CN=$\frac{9}{4}$|k|,CM=$\frac{1}{4}$|k|,然后根据△BCN∽△CAM得出$\frac{\frac{1}{2}}{\frac{9}{4}|k|}$=$\frac{\frac{1}{4}|k|}{\frac{3}{2}}$,从而求得k的值,即可求得反比例函数的解析式.
解答 解;(1)∵点C(-$\frac{1}{2}$,n+1)在直线y=k(x+$\frac{7}{4}$)上,
∴n+1=k(-$\frac{1}{2}$+$\frac{7}{4}$),整理得n+1=$\frac{5}{4}$k,
解得k=$\frac{4}{5}$(n+1);
(2)如图,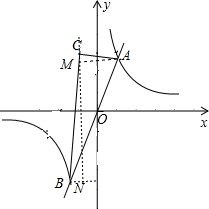 作CN∥y轴,交过B作y轴的垂线于N,过A作AM⊥CN于M,
作CN∥y轴,交过B作y轴的垂线于N,过A作AM⊥CN于M,
∵n+1=$\frac{5}{4}$k,
∴点C(-$\frac{1}{2}$,$\frac{5}{4}$k),
∵A(1,-k)和B(-1,k),
∴AM=1+$\frac{1}{2}$=$\frac{3}{2}$,BN=1-$\frac{1}{2}$=$\frac{1}{2}$,CN=$\frac{5}{4}$|k|+|k|=$\frac{9}{4}$|k|,CM=$\frac{5}{4}$|k|-|k|=$\frac{1}{4}$|k|,
∵∠ACB=90°,
∴∠BCN+∠ACM=90°,
∵∠BCN+∠CBN=90°,
∴∠CBN=∠ACM,
∵∠AMC=∠CNB=90°,
∴△BCN∽△CAM,
∴$\frac{BN}{CN}$=$\frac{CM}{AM}$,即$\frac{\frac{1}{2}}{\frac{9}{4}|k|}$=$\frac{\frac{1}{4}|k|}{\frac{3}{2}}$,
∴k2=$\frac{4}{3}$,
解得k=±$\frac{2}{3}$$\sqrt{3}$,
∴反比例函数的函数表达式为y=$\frac{2\sqrt{3}}{3x}$或y=-$\frac{2\sqrt{3}}{3x}$.
点评 本题考查了反比例函数图象上点的特征,主要是根据反比例函数的解析式表示出AM、BN、CM、CN的长度,进而根据三角形相似对应边成比例求出k的值,作出辅助线构建相似三角形是本题的关键.

| A. | a>b | B. | a<b | C. | a=b | D. | 不能确定 |
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{3y}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{3y}$ |