��Ŀ����
��ͼ����ƽ��ֱ������ϵ �У�ֱ��
�У�ֱ��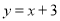 ��x����A�㣬��y����B�㣬��A��B�����������
��x����A�㣬��y����B�㣬��A��B����������� ��
�� ������һ��C����D�������ߵĶ���.
������һ��C����D�������ߵĶ���.

��1����������ߵĽ���ʽ��
��2����P��ֱ��AB�Ϸ�����������һ�㣬�������A��B�غϣ�������P�� ��Ĵ��߽�
��Ĵ��߽� ���ڵ�H����ֱ��AB�ڵ�F����PG��AB�ڵ�G������PFG���ܳ������P�������
���ڵ�H����ֱ��AB�ڵ�F����PG��AB�ڵ�G������PFG���ܳ������P�������
��3���������� ���Ƿ���ڳ���D����ĵ�M��ʹ�á�ABM���ABD�������ȣ� �����ڣ��������ʱ��M�����꣬�������ڣ���˵�����ɣ�
���Ƿ���ڳ���D����ĵ�M��ʹ�á�ABM���ABD�������ȣ� �����ڣ��������ʱ��M�����꣬�������ڣ���˵�����ɣ� 
��1�� ����2��P��
����2��P�� ��
�� ������3��M1����2��3����M2��
������3��M1����2��3����M2�� ��
�� ����M3��
����M3�� ��
�� ����
����
��������
�����������1������֪������������κ����Ľ���ʽ���ô���ϵ����ȷ�����κ����Ľ���ʽ���ɣ�
��2�����ȸ��ݡ�PFG�ǵ���ֱ�������Σ���P�� ��
�� ���õ�F��
���õ�F�� ��
�� ���������õ�PF=
���������õ�PF=
 ���Ӷ��õ���PFG�ܳ�Ϊ��
���Ӷ��õ���PFG�ܳ�Ϊ�� ���䷽��ȷ����P�����ꣻ
���䷽��ȷ����P�����ꣻ
��3����DM1��AB��M3M2��AB������AB�������ʱ������ͬ�ȸ߿���ȷ����ABM���ABD�������ȣ��ֱ����ֱ��DM1����ʽΪ�� ��ֱ��M3M2����ʽΪ��
��ֱ��M3M2����ʽΪ�� ������֮����ý������꼴�ɣ�
������֮����ý������꼴�ɣ�
�����������1����ֱ��AB�� �������ύ��A����3��0����B��0��3����
�������ύ��A����3��0����B��0��3����
���������߽���ʽ �У��ã�
�У��ã� ����ã�
����ã� ��
��
�������߽���ʽΪ�� ��
��
��2�����������֪��PFG�ǵ���ֱ�������Σ���P�� ��
�� ������F��
������F�� ��
�� ����
����
��PF=
 ��
��
��PFG�ܳ�Ϊ�� =
= ��
��
�൱ ʱ����PFG�ܳ������ֵ������
ʱ����PFG�ܳ������ֵ������ ʱ��
ʱ�� ����P��
����P�� ��
�� ����
����
��3����M������λ�ã���ͼ��ʾ��M1��M2��M3������ʹ��ABM��������ڡ�ABD�������
��ʱDM1��AB��M3M2��AB������AB������ȣ�
��D����1��4������E����1��2������N����1��0��
�� �У�k=1����ֱ��DM1����ʽΪ��
�У�k=1����ֱ��DM1����ʽΪ�� ��ֱ��M3M2����ʽΪ��
��ֱ��M3M2����ʽΪ�� ��
��
�� ��
�� ��
��
�� ��
�� ��
�� ��
�� ��
��
��M1����2��3����M2�� ��
�� ����M3��
����M3�� ��
�� ����
����

���㣺���κ����ۺ��⣮

 ��ҵ����ϵ�д�
��ҵ����ϵ�д� ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д� �����ܾ�ϵ�д�
�����ܾ�ϵ�д� ���ƿ�����ϵ�д�
���ƿ�����ϵ�д� ���̿ɻ�Ϊ �� ��
���̿ɻ�Ϊ �� �� B��
B��
 D��
D��

 ��
�� �ڵ������ޣ���P��ԭ��˳ʱ����ת90º��P
�ڵ������ޣ���P��ԭ��˳ʱ����ת90º��P
 ��
�� ������
������ �Ƿ���
�Ƿ��� �Ľ⣮
�Ľ⣮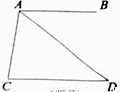
 �ĸ��� ��
�ĸ��� �� 
 ����
���� ��____________��
��____________��