题目内容
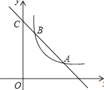
【题目】如图，直线
与双曲线
交于
两点，与
轴交于
点，已知
点的坐标为
，点坐标为
。
（1）求函数
的表达式和
点坐标；
（2）观察图像，当
时，直接写出
的取值范围。
【答案】（1）y1=-x+3，B（1,2）；（2）0<x<1或x>2
【解析】
（1）先把A（2，1），C（0，3）代入
，利用待定系数法可确定函数y1的表达式，再确定反比例函数解析式，然后解由两解析式所组成的方程组可确定B点坐标；
（2）由
可判断出，一次函数图象应在反比例函数图象下方，再观察函数图象可得到取值范围.
解：（1）将A（2,1）、C（0,3）代入得
，解得
，
∴
，
将A（2,1）代入
得
，
∴
解方程组
，得
或
∴B（1,2）；
（2）由图象可得，当
或
时，一次函数图象在反比例函数图象下方，
∴当时，
的取值范围是或.
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同)，现随机从中摸出10枚记下颜色后放回，这样连续做了10次，记录了如下的数据：
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 1 | 3 | 0 | 2 | 3 | 4 | 2 | 1 | 1 | 3 |
根据以上数据，估算袋中的白棋子数量为( )
A. 60枚 B. 50枚 C. 40枚 D. 30枚
【题目】某网店经市场调查，发现进价为40元的某新型文具每月的销售量y（件）与售价x（元）的相关信息如下：
售价x（元） | 60 | 70 | 80 | 90 | … |
销售量y（件） | 280 | 260 | 240 | 220 | … |
（1）试用你学过的函数来描述y与x的关系，这个函数可以是 （填“一次函数”、“反比例函数”或“二次函数”），并求这个函数关系式；
（2）当售价为多少元时，当月的销售利润最大，最大利润是多少；
（3）若获利不得高于进价的80%，那么售价定为多少元时，月销售利润达到最大，最大利润是多少？
