题目内容
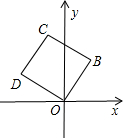 如图,四边形OBCD是边长为1的正方形,OB与x轴正半轴所成的角为60°,则点C的坐标为
如图,四边形OBCD是边长为1的正方形,OB与x轴正半轴所成的角为60°,则点C的坐标为分析:由正方形的边长可知OC的长,根据点C到点B和点O之间的距离,列出方程组进行求解即可.
解答:解:设C点的坐标为(a,b),
∵正方形OBCD的边长为1,
∴BC=1,OC=
,
∵OB与x轴正半轴所成的角为60°,OB=1,
∴点B的坐标为(
,
),
∴
,
解得:b=
(舍负值),a=
,
∴点C的坐标为(
-
,
+
).
∵正方形OBCD的边长为1,
∴BC=1,OC=
| 2 |
∵OB与x轴正半轴所成的角为60°,OB=1,
∴点B的坐标为(
| 1 |
| 2 |
| ||
| 2 |
∴
|
解得:b=
| ||
| 2 |
1-
| ||
| 2 |
∴点C的坐标为(
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
点评:根据线段之间的距离,列出方程组进行求解.

练习册系列答案
相关题目
 任意一点(与B、C不重合),过N作直线MN⊥x轴,垂足为A,MN交DC于M,设OA=t,OMN的面积为S.
任意一点(与B、C不重合),过N作直线MN⊥x轴,垂足为A,MN交DC于M,设OA=t,OMN的面积为S.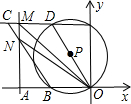 与点B,点C不重合),过N点作直线MN⊥x轴,垂足为A,交DC边于点M,设OA=t,△OMN的面积为S.
与点B,点C不重合),过N点作直线MN⊥x轴,垂足为A,交DC边于点M,设OA=t,△OMN的面积为S.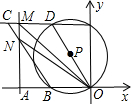 与点B,点C不重合),过N点作直线MN⊥x轴,垂足为A,交DC边于点M,设OA=t,△OMN的面积为S.
与点B,点C不重合),过N点作直线MN⊥x轴,垂足为A,交DC边于点M,设OA=t,△OMN的面积为S. 时,试判定直线MN与⊙P的位置关系,并说明理由.
时,试判定直线MN与⊙P的位置关系,并说明理由.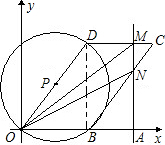 任意一点(与B、C不重合),过N作直线MN⊥x轴,垂足为A,MN交DC于M,设OA=t,OMN的面积为S.
任意一点(与B、C不重合),过N作直线MN⊥x轴,垂足为A,MN交DC于M,设OA=t,OMN的面积为S.