题目内容
 如图,把矩形纸片OABC放入平面直角坐标系中,使OC,OA分别落在x轴,y轴上,连接OB,将矩形纸片OABC沿OB折叠,使点A落在位A′的位置,A′B与x轴交于点D,若B点坐标为(4,2),则过点A′的反比例函数的解析式为________.
如图,把矩形纸片OABC放入平面直角坐标系中,使OC,OA分别落在x轴,y轴上,连接OB,将矩形纸片OABC沿OB折叠,使点A落在位A′的位置,A′B与x轴交于点D,若B点坐标为(4,2),则过点A′的反比例函数的解析式为________.
y=-
分析:根据翻折变换的性质以及勾股定理得出DO的长,进而利用△OA′D面积可得出A′E的长,进而得出A′点坐标,即可得出过点A′的反比例函数的解析式.
解答:由题意可得出:∠ABO=∠OBA′,
∵AB∥CO,
∴∠ABO=∠BOC,
∴∠A′BO=∠DOB,
∴DO=BD,
∵B点坐标为(4,2),
∴CO=4,BC=2,
设OD=x,则BD=x,DC=4-x,
在Rt△BDC中
BD2=CD2+BC2,
∴x2=(4-x)2+22,
解得:x=2.5,
∴A′D=4-2.5=1.5,OA′=AO=2,
过点A′作A′E⊥x轴于点E,作A′F⊥y轴于点F,
由△OA′D面积可得出:
∵A′E×DO=OA′×A′D,
∴A′E= =
= ,
,
∴OE= =
= ,
,
∴A′点坐标为:( ,-
,- ),
),
∴k= ×(-
×(- )=-
)=-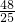 ,
,
∴过点A′的反比例函数的解析式为:y=- .
.
故答案为:y=- .
.
点评:此题主要考查了翻折变换的性质以及勾股定理的应用,得出BD=DO进而利用勾股定理得出DO的长是解题关键.

分析:根据翻折变换的性质以及勾股定理得出DO的长,进而利用△OA′D面积可得出A′E的长,进而得出A′点坐标,即可得出过点A′的反比例函数的解析式.
解答:由题意可得出:∠ABO=∠OBA′,
∵AB∥CO,
∴∠ABO=∠BOC,
∴∠A′BO=∠DOB,
∴DO=BD,
∵B点坐标为(4,2),
∴CO=4,BC=2,
设OD=x,则BD=x,DC=4-x,
在Rt△BDC中
BD2=CD2+BC2,

∴x2=(4-x)2+22,
解得:x=2.5,
∴A′D=4-2.5=1.5,OA′=AO=2,
过点A′作A′E⊥x轴于点E,作A′F⊥y轴于点F,
由△OA′D面积可得出:
∵A′E×DO=OA′×A′D,
∴A′E=
 =
= ,
,∴OE=
 =
= ,
,∴A′点坐标为:(
 ,-
,- ),
),∴k=
 ×(-
×(- )=-
)=-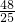 ,
,∴过点A′的反比例函数的解析式为:y=-
 .
.故答案为:y=-
 .
.点评:此题主要考查了翻折变换的性质以及勾股定理的应用,得出BD=DO进而利用勾股定理得出DO的长是解题关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
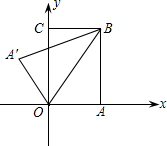 如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB将纸片沿OB折叠,使A落在A′的位置,若OB=
如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB将纸片沿OB折叠,使A落在A′的位置,若OB= ,tan∠BOC=
,tan∠BOC= ,则OA′=
,则OA′= 
 ,tan∠BOC=
,tan∠BOC= ,则OA′=
,则OA′= 

 ,tan∠BOC=
,tan∠BOC= ,则OA′=
,则OA′= 