题目内容
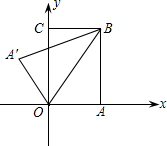如图，把矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y轴上，连接OB将纸片沿OB折叠，使A落在A′的位置，若OB=| 5 |
| 1 |
| 2 |
分析：如图所示，OABC构成矩形，则OA=BC，AB=OC，tan∠BOC=
=
=
．所以AB=2OA．
根据勾股定理得：OA=1．所以OA′=1．
| 1 |
| 2 |
| BC |
| OC |
| OA |
| AB |
根据勾股定理得：OA=1．所以OA′=1．
解答：解：∵OABC是矩形，
∴OA=BC，AB=OC，tan∠BOC=
=
=
，
∴AB=2OA．
∵OB2=AB2+OA2
∴OA=1．
∵OA′由OA翻折得到，
∴OA=OA′=1．
∴OA=BC，AB=OC，tan∠BOC=
| 1 |
| 2 |
| BC |
| OC |
| OA |
| AB |
∴AB=2OA．
∵OB2=AB2+OA2
∴OA=1．
∵OA′由OA翻折得到，
∴OA=OA′=1．
点评：此题考查折叠变换的性质．
练习册系列答案
名校课堂系列答案
相关题目
，tan∠BOC=
,则OA′= 
，tan∠BOC=
,则OA′= 
，tan∠BOC=
,则OA′= 