题目内容
20. 已知:如图,正方形ABCD中,P是对角线BD上的一个动点,PE⊥CD与E,PF⊥BC与F,连接EF.求证:AP=EF.
已知:如图,正方形ABCD中,P是对角线BD上的一个动点,PE⊥CD与E,PF⊥BC与F,连接EF.求证:AP=EF.
分析 连接CP,证矩形EPFC,求出EF=PC,证△ABP≌△CBP,推出AP=CP即可.
解答 证明:如图连接PC,
∵四边形ABCD是正方形,
∴∠C=90°,
∵PE⊥CD,PF⊥BC,
∴四边形PFCE是矩形,
∴EF=PC,
在△ABP和△CBP中$\left\{\begin{array}{l}{AB=BC}\\{∠ABP=∠CBP}\\{BP=BP}\end{array}\right.$
∴△ABP≌△CBP,
∴AP=CP,
∵EF=CP,
∴AP=EF.
点评 本题主要考查对勾股定理,全等三角形的性质和判定,正方形的性质等知识点的连接和掌握,能证出AP=PC是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11. 如图,四边形ABCD和四边形AEFC是两个平行四边形,点B在EF边上,若平行四边形ABCD和平行四边形AEFC的面积分别是s1,s2,则它们的大小关系是( )
如图,四边形ABCD和四边形AEFC是两个平行四边形,点B在EF边上,若平行四边形ABCD和平行四边形AEFC的面积分别是s1,s2,则它们的大小关系是( )
 如图,四边形ABCD和四边形AEFC是两个平行四边形,点B在EF边上,若平行四边形ABCD和平行四边形AEFC的面积分别是s1,s2,则它们的大小关系是( )
如图,四边形ABCD和四边形AEFC是两个平行四边形,点B在EF边上,若平行四边形ABCD和平行四边形AEFC的面积分别是s1,s2,则它们的大小关系是( )| A. | s1>s2 | B. | 2s1<s2 | C. | s1<s2 | D. | s1=s2 |
8. 如图所示为一个无盖长方体盒子的展开图(重叠部分不计),根据图中数据,可知该无盖长方体的容积为( )
如图所示为一个无盖长方体盒子的展开图(重叠部分不计),根据图中数据,可知该无盖长方体的容积为( )
 如图所示为一个无盖长方体盒子的展开图(重叠部分不计),根据图中数据,可知该无盖长方体的容积为( )
如图所示为一个无盖长方体盒子的展开图(重叠部分不计),根据图中数据,可知该无盖长方体的容积为( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
15.下列计算正确的是( )
| A. | -(-2)2=4 | B. | (a2b)3=a6b3 | C. | $\root{3}{64}$=8 | D. | |-4|=-4 |
9.不等式组-2≤x+1<1的解集,在数轴上表示正确的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
10.下列根式中,最简二次根式是( )
| A. | $\sqrt{9a}$ | B. | $\sqrt{{a^2}+{b^2}}$ | C. | $\sqrt{\frac{a}{3}}$ | D. | $\sqrt{0.5}$ |
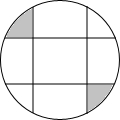 如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为π.
如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为π.