题目内容
如图，己知△ABC中，BC=60，BC边上的高AH=40；矩形DEFG的顶点D、E在边 BC上，顶点G、F分别在边AB、AC上，设EF的长为x，矩形DEFG的面积为y．求y关于x的函数关系式，并指出这个函数的定义域．
解：∵EF=x，AH=40，
∴AM=40-x，
∵矩形DEFG的顶点D、E在边 BC上，顶点G、F分别在边AB、AC上，
∴GF∥BC，
∴△AGF∽△ABC，
∴
=
，即
=
，
∴GF=60-
x，
∴y=EF•GF=x（60-x），即y=-x2+60x（0＜x＜40）．
分析：先根据相似三角形的判定定理得出△AGF∽△ABC，那么它们的对应边和对应高的比相等，可据此求出AM的表达式，进而可求出GF的长，已知矩形的长和宽，即可根据矩形的面积公式得到y、x的函数关系式．
点评：本题考查的是相似三三角形在实际生活中的应用及矩形的面积，熟知相似三角形对应边成比例的性质是解答此题的关键．
∴AM=40-x，
∵矩形DEFG的顶点D、E在边 BC上，顶点G、F分别在边AB、AC上，
∴GF∥BC，
∴△AGF∽△ABC，
∴
=，即=，∴GF=60-
x，∴y=EF•GF=x（60-
x），即y=-x2+60x（0＜x＜40）．分析：先根据相似三角形的判定定理得出△AGF∽△ABC，那么它们的对应边和对应高的比相等，可据此求出AM的表达式，进而可求出GF的长，已知矩形的长和宽，即可根据矩形的面积公式得到y、x的函数关系式．
点评：本题考查的是相似三三角形在实际生活中的应用及矩形的面积，熟知相似三角形对应边成比例的性质是解答此题的关键．
练习册系列答案
相关题目
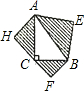己知，如图，在Rt△ABC中，∠C=90°，以Rt△ABC的三边为斜边分别向外作三个等腰直角三角形，其中∠H、∠E、∠F是直角，若斜边AB=3，则图中阴影部分的面积为（ ）
请在画出的三角形的顶点处标上相对应的字母！）
（2012•嘉定区一模）如图，己知△ABC中，BC=60，BC边上的高AH=40；矩形DEFG的顶点D、E在边 BC上，顶点G、F分别在边AB、AC上，设EF的长为x，矩形DEFG的面积为y．求y关于x的函数关系式，并指出这个函数的定义域．