题目内容
【题目】(1)观察与发现:
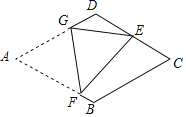
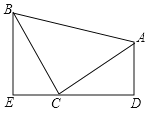
小明将三角形纸片![]() (
(![]() )沿过点
)沿过点![]() 的直线折叠,使得
的直线折叠,使得![]() 落在
落在![]() 边上,折痕为
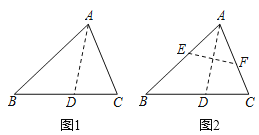
边上,折痕为![]() ,展开纸片(如图1);在第一次的折叠基础上第二次折叠该三角形纸片,使点
,展开纸片(如图1);在第一次的折叠基础上第二次折叠该三角形纸片,使点![]() 和点
和点![]() 重合,折痕为
重合,折痕为![]() ,展平纸片后得到
,展平纸片后得到![]() (如图2).小明认为
(如图2).小明认为![]() 是等腰三角形,你同意他的结论吗?请说明理由:
是等腰三角形,你同意他的结论吗?请说明理由:
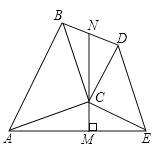
(2)模型与运用:
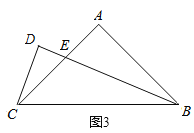
如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .若
.若![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)同意,理由详见解析;(2)16.
【解析】
(1)方法一由两次折叠知,点A在EF的中垂线上,所以AE=AF;方法二根据折叠可得![]() ,进而求解;
,进而求解;
(2)延长![]() 与
与![]() 并交于点
并交于点![]() ,由折叠的性质可得
,由折叠的性质可得![]() ,进而得出
,进而得出![]() ,最后利用三角形的面积公式求解即可.
,最后利用三角形的面积公式求解即可.
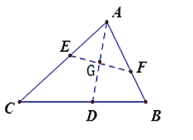
解:(1)理由如下:
如图,设![]() 与
与![]() 交于点
交于点![]() ,
,
由折叠知,![]() 平分
平分![]() ,
,
所以![]() .
.
由折叠知,![]() ,
,
所以![]()
所以![]()
所以![]() .
.
即![]() 为等腰三角形.
为等腰三角形.
方法2:解:理由如下:
如图,设![]() 与
与![]() 交于点
交于点![]() .
.
由折叠知,![]() 平分
平分![]() ,
,
所以![]() .
.
由折叠知,![]() ,
,
所以![]() ,
,
在![]() 和
和![]() 中,
中,
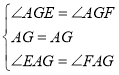
所以![]()
所以![]() ,
,
即![]() 为等腰三角形
为等腰三角形
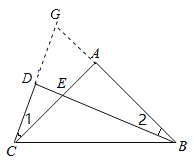
(2)延长![]() 与
与![]() 并交于点
并交于点![]() ,
,
由(1)知![]() ,
,
又![]() 平分
平分![]()
![]() 是
是![]() 的中线
的中线
即![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

练习册系列答案
相关题目