题目内容
【题目】如图，在
中，
．
（1）尺规作图：以
为直径作
，分别交
和
于点
和
．(保留作图痕迹，不写做法)
（2）过作
，垂足为
①求证：
为的切线．
②连接
，若
，
，求的半径长．
【答案】（1）画图见解析；（2）①证明见解析，②2．
【解析】
（1）根据题意，以
为直径作
，分别交
和
于点
和
作图即可．
（2）①作AB的中点O，连接OE、AE，根据等腰三角形的性质可得
，再根据圆周角定理可得
，即可得
，
，再根据余角的性质可得
，再根据等腰三角形的性质可得
，从而得出
，即可得证
为的切线．②过点O作
，根据垂径定理得到D为AF的中点，设圆的半径为r，表示出AF，AD以及HD，在直角三角形OAD中，表示出OD2，在直角三角形ODH中，利用勾股定理列出关于r的方程，求出方程的解即可．
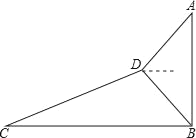
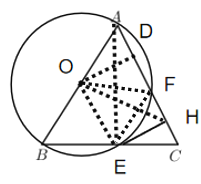
（1）如图所示，即为所求．
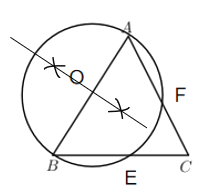
（2）①作AB的中点O，连接OE、AE
∵
∴
∵AB是的直径
∴
∴，
∵
∴
∴
∴
∵OA、OE是圆的半径
∴
∴
∴
∴为的切线
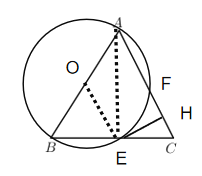
②连接
，过点O作
∵AB是圆O的直径
∵EH是圆O的切线
∴
∵OA、OF为圆的半径
∴
∵
∴
设圆的半径为r，则
∴
∴
在Rt△AOD中，根据勾股定理得
在Rt△ODH中，根据勾股定理得
即
解得
（舍去）或
则圆的半径为2．
练习册系列答案
相关题目
