题目内容
如图1,△ABC内接于半径为4cm的⊙O,AB为直径,弧BC长为
cm.
(1)计算∠ABC的度数;
(2)将与△ABC全等的△FED如图2摆放,使两个三角形的对应边DF与AC有一部分重叠,△FED的最长边EF恰好经过弧AB的中点M.求证:AF=AB.

| 4π |
| 3 |
(1)计算∠ABC的度数;
(2)将与△ABC全等的△FED如图2摆放,使两个三角形的对应边DF与AC有一部分重叠,△FED的最长边EF恰好经过弧AB的中点M.求证:AF=AB.

考点:圆周角定理,全等三角形的判定与性质,弧长的计算
专题:
分析:(1)连结OC,设∠BOC=n°,根据扇形的弧长公式求出n的度数;
(2)连结OM,过点F作FH⊥AB于H,构造Rt△FAH,根据直角三角形的性质的出FH=
AF,由垂径定理的出OM=
AB,再根据△ABC≌△FED全等得出∠A=∠EFD=30°,故EF∥AB,OM=FH=
AB,由此可得出结论.
(2)连结OM,过点F作FH⊥AB于H,构造Rt△FAH,根据直角三角形的性质的出FH=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:(1)如图1,连结OC,设∠BOC=n°,
解:(1)如图1,连结OC,设∠BOC=n°,
∵
长为
cm,⊙O的半径为4cm,
∴
=
,
∴n=60,即∠BOC=60°,
∵OB=OC,
∴∠ABC=∠OBC=
=60°,
(2)如图2,连结OM,过点F作FH⊥AB于H,
∵AB为直径,
∴∠ACB=90°,
∴∠A=180°-90°-60°=30°,
∴在Rt△FAH中,FH=
AF,
∵点M为
的中点,
∴OM⊥AB且OM=
AB,
∵△ABC≌△FED全等,
∴∠A=∠EFD=30°,
∴EF∥AB,OM=FH=
AB,
∴AF=AB.
 解:(1)如图1,连结OC,设∠BOC=n°,
解:(1)如图1,连结OC,设∠BOC=n°,∵
 |
| BC |
| 4π |
| 3 |
∴
| 4×nπ |
| 180 |
| 4π |
| 3 |
∴n=60,即∠BOC=60°,
∵OB=OC,
∴∠ABC=∠OBC=
| 180-60 |
| 2 |
(2)如图2,连结OM,过点F作FH⊥AB于H,
∵AB为直径,
∴∠ACB=90°,
∴∠A=180°-90°-60°=30°,
∴在Rt△FAH中,FH=
| 1 |
| 2 |
∵点M为
 |
| AB |
∴OM⊥AB且OM=
| 1 |
| 2 |
∵△ABC≌△FED全等,
∴∠A=∠EFD=30°,
∴EF∥AB,OM=FH=
| 1 |
| 2 |
∴AF=AB.
点评:本题考查的是圆周角定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
要了解某地农户用电情况,抽查了部分农户在某地一个月中用电情况:用电15度的有3户,用电20度的有5户,用电30度的有7户,那么平均每户用电( )
| A、23.7度 | B、21.6度 |
| C、20度 | D、5.416度 |

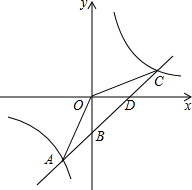 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y= 如图,在△ABC中,∠ABC=2∠C,AD平分∠BAC,求证:AB+BD=AC.
如图,在△ABC中,∠ABC=2∠C,AD平分∠BAC,求证:AB+BD=AC. 如图,在△ABC中,AD平分∠BAC且与BC相交于点D,∠B=40°,∠BAD=30°,则∠C的度数是多少?
如图,在△ABC中,AD平分∠BAC且与BC相交于点D,∠B=40°,∠BAD=30°,则∠C的度数是多少?