题目内容
如图,已知抛物线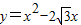 ,等边△ABC的边长为
,等边△ABC的边长为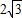 ,顶点A在抛物线上滑动,且BC边始终平行水平方向,当△ABC在滑动过程中,点B落在坐标轴上时,C点坐标是: .
,顶点A在抛物线上滑动,且BC边始终平行水平方向,当△ABC在滑动过程中,点B落在坐标轴上时,C点坐标是: .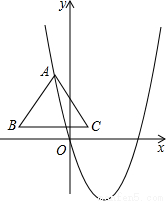
【答案】分析:根据等边三角形的边长解直角三角形求出等边三角形的高为3,然后分①点B在x轴上时,点A的坐标为纵坐标为3,代入抛物线解析式求出点A的横坐标,根据等边三角形的性质,然后利用等边三角形的性质解答即可;②点B在y轴上时,点A的横坐标为等边三角形边长的一半,即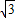 ,然后代入抛物线解析式求出点A的纵坐标,再向下3个单位长度即为点C的纵坐标,点C的横坐标的长度等于等边三角形的边长,写出即可.
,然后代入抛物线解析式求出点A的纵坐标,再向下3个单位长度即为点C的纵坐标,点C的横坐标的长度等于等边三角形的边长,写出即可.
解答: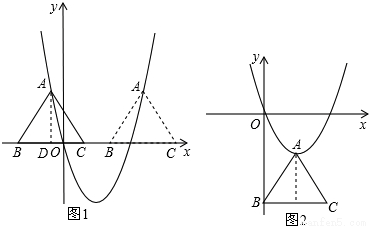 解:∵等边△ABC的边长为
解:∵等边△ABC的边长为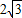 ,
,
∴高线AD=2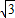 ×
×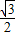 =3,边长的一半为
=3,边长的一半为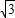 ,
,
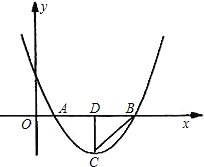
①如图1,点B在x轴上时,点A的纵坐标为3,
∵点A在抛物线上滑动,
∴x2-2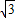 x=3,
x=3,
整理得,x2-2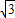 x-3=0,
x-3=0,
解得x=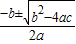 =
=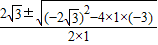 =
=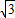 ±
±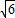 ,
,
当x=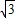 -
- 时,
时,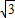 -
-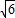 +
+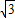 =2
=2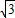 -
- ,
,
此时,点C的坐标为(2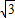 -
-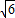 ,0),
,0),
当x=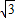 +
+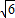 时,
时,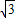 +
+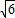 +
+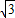 =2
=2 +
+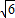 ,
,
此时,点C的坐标为(2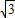 +
+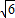 ,0);
,0);
②如图2,点B在y轴上时,点A的横坐标等于等边三角形边长的一半,为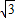 ,
,
∵点A在抛物线上滑动,
∴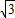 2-2
2-2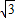 ×
×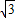 =3-6=-3,
=3-6=-3,
-3-3=-6,
所以点C的坐标为(2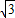 ,-6),
,-6),
综上所述,点C的坐标为(2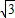 -
-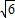 ,0),(2
,0),(2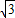 +
+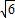 ,0),(2
,0),(2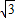 ,-6).
,-6).
故答案为:(2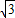 -
-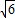 ,0),(2
,0),(2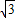 +
+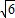 ,0),(2
,0),(2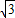 ,-6).
,-6).
点评:本题综合考查了二次函数问题,等边三角形的性质,难点在于要分点在x轴上与y轴上两种情况讨论求解.
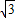 ,然后代入抛物线解析式求出点A的纵坐标,再向下3个单位长度即为点C的纵坐标,点C的横坐标的长度等于等边三角形的边长,写出即可.
,然后代入抛物线解析式求出点A的纵坐标,再向下3个单位长度即为点C的纵坐标,点C的横坐标的长度等于等边三角形的边长,写出即可.解答:
 解:∵等边△ABC的边长为
解:∵等边△ABC的边长为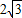 ,
,∴高线AD=2
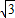 ×
×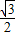 =3,边长的一半为
=3,边长的一半为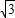 ,
,①如图1,点B在x轴上时,点A的纵坐标为3,
∵点A在抛物线上滑动,
∴x2-2
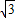 x=3,
x=3,整理得,x2-2
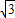 x-3=0,
x-3=0,解得x=
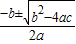 =
=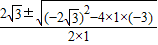 =
=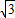 ±
±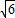 ,
,当x=
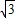 -
- 时,
时,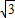 -
-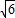 +
+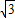 =2
=2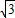 -
- ,
,此时,点C的坐标为(2
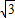 -
-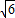 ,0),
,0),当x=
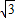 +
+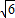 时,
时,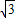 +
+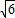 +
+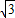 =2
=2 +
+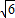 ,
,此时,点C的坐标为(2
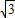 +
+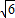 ,0);
,0);②如图2,点B在y轴上时,点A的横坐标等于等边三角形边长的一半,为
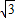 ,
,∵点A在抛物线上滑动,
∴
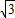 2-2
2-2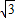 ×
×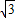 =3-6=-3,
=3-6=-3,-3-3=-6,
所以点C的坐标为(2
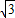 ,-6),
,-6),综上所述,点C的坐标为(2
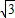 -
-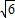 ,0),(2
,0),(2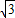 +
+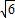 ,0),(2
,0),(2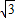 ,-6).
,-6).故答案为:(2
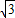 -
-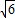 ,0),(2
,0),(2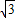 +
+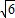 ,0),(2
,0),(2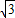 ,-6).
,-6).点评:本题综合考查了二次函数问题,等边三角形的性质,难点在于要分点在x轴上与y轴上两种情况讨论求解.

练习册系列答案
相关题目
 对称轴与x轴的交点.
对称轴与x轴的交点.
 如图,已知抛物线C1的顶点坐标是D(1,4),且经过点C(2,3),又与x轴交于点A、E(点A在点E左边),与y轴交于点B.
如图,已知抛物线C1的顶点坐标是D(1,4),且经过点C(2,3),又与x轴交于点A、E(点A在点E左边),与y轴交于点B.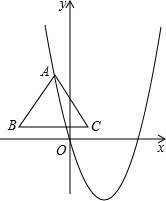 如图,已知抛物线
如图,已知抛物线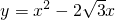 ,等边△ABC的边长为
,等边△ABC的边长为 ,顶点A在抛物线上滑动,且BC边始终平行水平方向,当△ABC在滑动过程中,点B落在坐标轴上时,C点坐标是:________.
,顶点A在抛物线上滑动,且BC边始终平行水平方向,当△ABC在滑动过程中,点B落在坐标轴上时,C点坐标是:________.