题目内容
两次分别从1~6六个整数中任取一个数,第一个数作为点P(m,n)的横坐标,第二个数作为点P(m,n)的纵坐标,则点P(m,n)在反比例函数y=
的图象上的概率是
.
| 12 |
| x |
| 1 |
| 9 |
| 1 |
| 9 |
分析:画出树状图求出所有情况数,再根据反比例函数图象上点的坐标特征验证在函数图象上的点的情况数,然后根据概率公式列式计算即可得解.
解答:解:

所以共有36种情况,
∵反比例函数y=
的图象上的点的坐标满足xy=12,
∴在反比例函数图象上的点有(2,6)(3,4)(4,6)(6,2),共4个,
P=
=
.
故答案为:
.

所以共有36种情况,
∵反比例函数y=
| 12 |
| x |
∴在反比例函数图象上的点有(2,6)(3,4)(4,6)(6,2),共4个,
P=
| 4 |
| 36 |
| 1 |
| 9 |
故答案为:
| 1 |
| 9 |
点评:本题考查的是用画树状图法求概率,以及反比例函数图象上的点的坐标特征,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
 的横坐标,第二个数作为点
的横坐标,第二个数作为点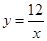 的图象上的概率一定大于在反比例函数
的图象上的概率一定大于在反比例函数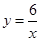 的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?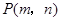 的横坐标,第二个数作为点
的横坐标,第二个数作为点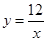 的的图象上的概率一定大于在反比例函数
的的图象上的概率一定大于在反比例函数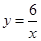 的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?