题目内容
【题目】如图,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N.下列结论:①AF⊥BG;②BN= ![]() NF;③
NF;③ ![]() =
= ![]() ;④S四边形CGNF=
;④S四边形CGNF= ![]() S四边形ANGD . 其中正确的结论的序号是 .
S四边形ANGD . 其中正确的结论的序号是 . 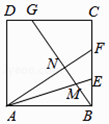
【答案】①③
【解析】解:①∵四边形ABCD为正方形, ∴AB=BC=CD,
∵BE=EF=FC,CG=2GD,
∴BF=CG,
∵在△ABF和△BCG中,  ,
,
∴△ABF≌△BCG,
∴∠BAF=∠CBG,
∵∠BAF+∠BFA=90°,
∴∠CBG+∠BFA=90°,即AF⊥BG;①正确;②∵在△BNF和△BCG中, ![]() ,
,
∴△BNF∽△BCG,∴ ![]() =
= ![]() =
= ![]() ,
,
∴BN= ![]() NF;②错误;③作EH⊥AF,令AB=3,则BF=2,BE=EF=CF=1,
NF;②错误;③作EH⊥AF,令AB=3,则BF=2,BE=EF=CF=1,
AF= ![]() =
= ![]() ,
,
∵S△ABF= ![]() AFBN=
AFBN= ![]() ABBF,
ABBF,
∴BN= ![]() ,NF=
,NF= ![]() BN=
BN= ![]() ,
,
∴AN=AF﹣NF= ![]() ,
,
∵E是BF中点,
∴EH是△BFN的中位线,
∴EH= ![]() ,NH=
,NH= ![]() ,BN∥EH,
,BN∥EH,
∴AH= ![]() ,
, ![]() =
= ![]() ,解得:MN=
,解得:MN= ![]() ,
,
∴BM=BN﹣MN= ![]() ,MG=BG﹣BM=
,MG=BG﹣BM= ![]() ,
,
∴ ![]() =
= ![]() ;③正确;
;③正确;
④连接AG,FG,根据③中结论,
则NG=BG﹣BN= ![]() ,
,
∵S四边形CGNF=S△CFG+S△GNF= ![]() CGCF+
CGCF+ ![]() NFNG=1+
NFNG=1+ ![]() =
= ![]() ,
,
S四边形ANGD=S△ANG+S△ADG= ![]() ANGN+
ANGN+ ![]() ADDG=
ADDG= ![]() +
+ ![]() =
= ![]() ,
,
∴S四边形CGNF≠ ![]() S四边形ANGD , ④错误;
S四边形ANGD , ④错误;
所以答案是①③.
【考点精析】利用正方形的性质和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案