��Ŀ����
����Ŀ����ͼ��ij��ѧ�С��Ϊ����ѧУ���AB�ĸ߶ȣ��������ǰ��2 ![]() �״��ĵ�C��������б���¶�i=1��
�״��ĵ�C��������б���¶�i=1�� ![]() ��б��CDǰ��4�����D���ڵ�D�����ò���ǣ������˶���A������Ϊ37�㣬���������ĸ�DEΪ1.5�ף���֪A��B��C��D��E��ͬһƽ���ڣ�AB��BC��AB��DE�������AB�ĸ߶ȣ����ο����ݣ�sin37���
��б��CDǰ��4�����D���ڵ�D�����ò���ǣ������˶���A������Ϊ37�㣬���������ĸ�DEΪ1.5�ף���֪A��B��C��D��E��ͬһƽ���ڣ�AB��BC��AB��DE�������AB�ĸ߶ȣ����ο����ݣ�sin37��� ![]() ��cos37���
��cos37��� ![]() ��tan37���
��tan37��� ![]() ���������������ţ�
���������������ţ�
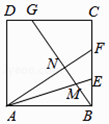
���𰸡��⣺��ͼ���ӳ�ED��BC�ӳ����ڵ�F�����CFD=90�㣬
��tan��DCF=i= ![]() =
= ![]() ��
��
���DCF=30�㣬
��CD=4��
��DF= ![]() CD=2��CF=CDcos��DCF=4��
CD=2��CF=CDcos��DCF=4�� ![]() =2
=2 ![]() ��
��
��BF=BC+CF=2 ![]() +2
+2 ![]() =4
=4 ![]() ��
��
����E��EG��AB�ڵ�G��
��GE=BF=4 ![]() ��GB=EF=ED+DF=1.5+2=3.5��
��GB=EF=ED+DF=1.5+2=3.5��
�֡ߡ�AED=37�㣬
��AG=GEtan��AEG=4 ![]() tan37�㣬
tan37�㣬
��AB=AG+BG=4 ![]() tan37��+3.5=3
tan37��+3.5=3 ![]() +3.5��
+3.5��
�����AB�ĸ߶�Ϊ��3 ![]() +3.5����
+3.5����
���������ӳ�ED��BC�ӳ����ڵ�F�����CFD=90�㣬Rt��CDF�����CF=CDcos��DCF=2 ![]() ��DF=
��DF= ![]() CD=2����EG��AB���ɵ�GE=BF=4
CD=2����EG��AB���ɵ�GE=BF=4 ![]() ��GB=EF=3.5�������AG=GEtan��AEG=4
��GB=EF=3.5�������AG=GEtan��AEG=4 ![]() tan37��ɵô𰸣�
tan37��ɵô𰸣�
�����㾫����������Ŀ����֪���������ù��ڷ������������֪ʶ���Եõ�����Ĵ𰸣���Ҫ����ָ����ָ�Ϸ�������Ŀ�귽�� �����ɵ�С��90���ˮƽ�ǣ���������ǣ�

 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�