题目内容
15.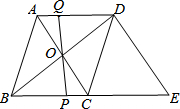 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,P为线段BC上一点(除端点外),连接PO并延长交AD于点Q,延长BC到点E,使CE=BC,连接DE.
如图,在平行四边形ABCD中,对角线AC与BD相交于点O,P为线段BC上一点(除端点外),连接PO并延长交AD于点Q,延长BC到点E,使CE=BC,连接DE.(1)求证:BP=DQ;
(2)已知AB=5,AC=6,若CD=$\frac{1}{2}$BE,求△BDE的周长.
分析 (1)由平行四边形的性质得出AD∥BC,OB=OD,AD=BC,CD=AB,得出∠OBP=∠ODQ,由ASA证明△BOP≌△DOQ,得出对应边相等即可;
(2)先证明四边形ACED是平行四边形,得出DE=AC=6,再证明△BDE是直角三角形,根据勾股定理求出BD,即可得出结果.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OB=OD,AD=BC,CD=AB,
∴∠OBP=∠ODQ,
在△BOP和△DOQ中,
$\left\{\begin{array}{l}{∠OBP=∠ODQ}&{\;}\\{OB=OD}&{\;}\\{∠BOP=∠DOQ}&{\;}\end{array}\right.$,
∴△BOP≌△DOQ(ASA),
∴BP=DQ;
(2)解:∵AD=BC,CE=BC,
∴AD=CE=BC,
∵AD∥BC,
∴AD∥CE,
∴四边形ACED是平行四边形,
∴DE=AC=6,
∵CD=$\frac{1}{2}$BE,
∴∠BDE=90°,BE=2CD=2AB=10,
∴BD=$\sqrt{B{E}^{2}-D{E}^{2}}$=$\sqrt{{{10}^2}-{6^2}}$=8,
∴△BDE的周长=BD+BE+DE=8+10+6=24.
点评 本题考查了平行四边形的性质与判定、全等三角形的判定与性质、勾股定理、三角形周长的计算;熟练掌握平行四边形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
相关题目
5.直角坐标系中点P(a+2,a-2)不可能所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.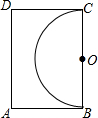 如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
 如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )| A. | 9m | B. | 7m | C. | 5m | D. | 3m |
20.以下问题,不适合用全面调查的是( )
| A. | 了解一批灯泡的使用寿命 | B. | 学校招聘教师,对应聘人员的面试 | ||
| C. | 了解全校学生的课外读书时间 | D. | 旅客上飞机前的安检 |
7.若点P在第二象限,点P到x 轴的距离是7,到y轴的距离是3,点P的坐标是( )
| A. | (-7,3) | B. | (7,-3) | C. | (-3,7) | D. | (3,-7) |
4.把点(2,-3)先向左平移3个单位长度,再向下平移2个单位长度得到的点的坐标是( )
| A. | (-1,-5) | B. | (5,-1) | C. | (5,-5) | D. | (-1,-1) |
5.下列计算正确的是( )
| A. | a•a3=a3 | B. | a4+a3=a2 | C. | (a2)5=a7 | D. | (-ab)2=a2b2 |