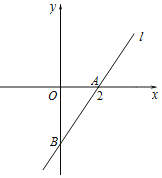Question

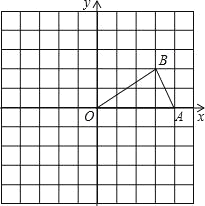
【题目】二次函数y＝ax2+bx+c的图象如图所示，经过（﹣1，0）、（3，0）、（0，﹣3）．

（1）求二次函数的解析式；

（2）不等式ax2+bx+c＞0的解集为　 　；

（3）方程ax2+bx+c＝m有两个实数根，m的取值范围为　 　．

Answer 1

【答案】（1）y＝x2﹣2x﹣3；（2）x＜﹣1或x＞3；（3）m≥﹣4．

【解析】

（1）把（﹣1，0）、（3，0）、（0，﹣3）代入y＝ax2+bx+c解方程组即可得到结论；

（2）根据图象即可得到结论；

（3）设y＝ax2+bx+c和y＝m，方程ax2+bx+c＝m有两个实数根，即二次函数图象与直线y＝m有两个交点或一个交点，结合一元二次方程根的判别式即可求出m的取值范围．

解：（1）把（﹣1，0）、（3，0）、（0，﹣3）代入y＝ax2+bx+c得，

解得：，

∴二次函数的解析式为y＝x2﹣2x﹣3；

（2）由函数图象可知抛物线和x轴的两个交点横坐标为﹣1，3，

所以不等式ax2+bx+c＞0的解集为x＜﹣1或x＞3；

（3）设y＝ax2+bx+c和y＝m，

方程ax2+bx+c＝m有两个实数根，则二次函数图象与直线y＝m有两个交点或一个交点，

即有两个实数根，

∴，即，

解得m≥﹣4．