题目内容
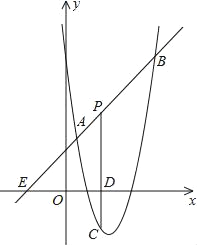
【题目】如图，已知点A在反比例函数
（x＞0）的图像上，过点A作AC⊥x轴，垂足是C，AC=OC．一次函数y=kx+b的图像经过点A，与y轴的正半轴交于点B．
（1）求点A的坐标；
（2）若四边形ABOC的面积是
，求一次函数y=kx+b的表达式．
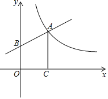
【答案】（1）
；（2）y=
+2
【解析】
（1）由AC=OC，设A（m,m）代入反比例函数得m2=9，求出A点坐标；
（2）利用四边形ABOC的面积求出B点坐标，再用待定系数法确定函数关系式即可求出AB的解析式.
（1）∵AC=OC
∴可设A（m,m）
∵点A（m,m）在y=
的图像上
∴m2=9
∴m=±3
∵x＞0
∴m=3
（2）∵AC⊥x轴，OB⊥x轴
∴ S四边形ABOC=
=(3+OB)·3
=
∴OB=2
∴B（0，2）
∵y=kx+b过点A（3，3），B（0，2）
∴
∴
∴一次函数的表达式为y=
+2
练习册系列答案
名校课堂系列答案
相关题目
