题目内容
点A的坐标为(
,0),把点A绕着坐标原点顺时针旋转135°到点B,那么点B的坐标是
-
=
| 2 |
(1,-1)
(1,-1)
.计算:| x2 |
| x+1 |
| 1 |
| x+1 |
x-1
x-1
.分析:过点B作BC⊥x轴于C,根据旋转角求出∠BOC=45°,从而得到△BOC是等腰直角三角形,然后求出OC=BC=1,再根据点B在第四象限写出坐标即可;
根据同分母分式相减,分母不变,分子相减,然后把分子分解因式,再约分即可.
根据同分母分式相减,分母不变,分子相减,然后把分子分解因式,再约分即可.
解答: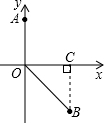 解:如图,过点B作BC⊥x轴于C,
解:如图,过点B作BC⊥x轴于C,
∵点A绕着坐标原点顺时针旋转135°到点B,
∴∠BOC=45°,
∴△BOC是等腰直角三角形,
∵点A的坐标为(
,0),
∴OB=OA=
,
∴OC=BC=
×
=1,
∵点B在第四象限,
∴点B(1,-1);
-
=
=
=x-1.
故答案为:(1,-1);x-1.
 解:如图,过点B作BC⊥x轴于C,
解:如图,过点B作BC⊥x轴于C,∵点A绕着坐标原点顺时针旋转135°到点B,
∴∠BOC=45°,
∴△BOC是等腰直角三角形,
∵点A的坐标为(
| 2 |
∴OB=OA=
| 2 |
∴OC=BC=
| 2 |
| ||
| 2 |
∵点B在第四象限,
∴点B(1,-1);
| x2 |
| x+1 |
| 1 |
| x+1 |
| x2-1 |
| x+1 |
| (x+1)(x-1) |
| x+1 |
故答案为:(1,-1);x-1.
点评:本题考查了坐标与图形变化-旋转,分式的加减运算,作辅助线构造出等腰直角三角形是解题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图所示,在Rt△OAB中,∠OAB=90°,且点B的坐标为(4,2).画出△OAB绕点O逆时针旋转90°后的△OA1B1,并求出AA1的长.
如图所示,在Rt△OAB中,∠OAB=90°,且点B的坐标为(4,2).画出△OAB绕点O逆时针旋转90°后的△OA1B1,并求出AA1的长.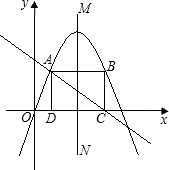 线
线
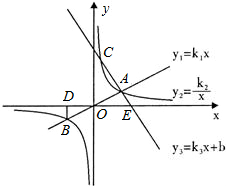 如图,正比例函数y1=k1x与反比例函数y2=
如图,正比例函数y1=k1x与反比例函数y2=