题目内容
(1)如图,在平行四边形ABCD中,点E,F是对角线BD上两点,且BF=DE.写出图中一对全等的三角形并加以证明

(2)如图.在三角形ABC中,∠A=45°,tanB= ,BC=
,BC= ,求AB的长.
,求AB的长.

解:(1)△BFA≌△DEC.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABF=∠CDE,
∵BF=DE.
∴△BFA≌△DEC;
(2)作CD垂直于AB于点D.
设CD为x,
∵tanB= ,
,
∴BD为3x,
∵BC= ,
,
∴CD=1,
∴BD=3,
∵∠A=45°,
∴AD=CD=1,
∴AB=AD+BD=1+3=4.
分析:(1)可选择△BFA≌△DEC,利用角边角的知识证明即可;
(2)可设CD为x,利用tanB可得BD,利用勾股定理可得x的值,进而求得BD,AD的值,相加即可.
点评:考查三角形全等的判定及解直角三角形的知识;构造直角三角形作出相应辅助线是解决本题的难点.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABF=∠CDE,
∵BF=DE.
∴△BFA≌△DEC;
(2)作CD垂直于AB于点D.

设CD为x,
∵tanB=
 ,
,∴BD为3x,
∵BC=
 ,
,∴CD=1,
∴BD=3,
∵∠A=45°,
∴AD=CD=1,
∴AB=AD+BD=1+3=4.
分析:(1)可选择△BFA≌△DEC,利用角边角的知识证明即可;
(2)可设CD为x,利用tanB可得BD,利用勾股定理可得x的值,进而求得BD,AD的值,相加即可.
点评:考查三角形全等的判定及解直角三角形的知识;构造直角三角形作出相应辅助线是解决本题的难点.

练习册系列答案
相关题目
 30、如图,在平行四边形ABCD中,O是对角线AC的中点,过O点作直线EF分别交BC、AD于E、F.
30、如图,在平行四边形ABCD中,O是对角线AC的中点,过O点作直线EF分别交BC、AD于E、F.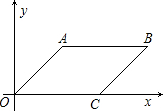 如图,在平行四边形ABC0中,已知点A、C两点的坐标为A(
如图,在平行四边形ABC0中,已知点A、C两点的坐标为A( 接DE,交OC于点F,作FG∥AB,交BC于点G.
接DE,交OC于点F,作FG∥AB,交BC于点G.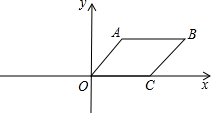 如图,在平行四边形OABC中,已知
如图,在平行四边形OABC中,已知 如图,在平行四边形ABCD中,E、F分别为AB、CD的中点,连接DE、EF、FB,则图中共有平行四才边形的个数(平行四边形ABCD除外)为( )
如图,在平行四边形ABCD中,E、F分别为AB、CD的中点,连接DE、EF、FB,则图中共有平行四才边形的个数(平行四边形ABCD除外)为( )