Question

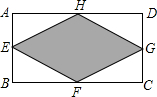已知：如图，在矩形ABCD中，E，F，G，H分别为边AB，BC，CD，DA的中点．若AB=2，AD=4，则图中阴影部分的面积为

4

．

Answer 1

分析：连接AC，BD，FH，EG，得出平行四边形ABFH，推出HF=AB=2，同理EG=AD=4，求出四边形EFGH是菱形，根据菱形的面积等于

1

2

×GH×HF，代入求出即可．

解答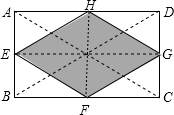：解：连接AC，BD，FH，EG，
∵E，F，G，H分别为边AB，BC，CD，DA的中点，
∴AH=

1

2

AD，BF=

1

2

BC，
∵四边形ABCD是矩形，
∴AD=BC，AD∥BC，
∴AH=BF，AH∥BF，
∴四边形AHFB是平行四边形，
∴FH=AB=2，
同理EG=AD=4，
∵四边形ABCD是矩形，
∴AC=BD，
∵E，F，G，H分别为边AB，BC，CD，DA的中点，
∴HG∥AC，HG=

1

2

AC，EF∥AC，EF=

1

2

AC，EH=

1

2

BD，
∴EH=HG，GH=EF，GH∥EF，
∴四边形EFGH是平行四边形，
∴平行四边形EFGH是菱形，
∴FH⊥EG，
∴阴影部分EFGH的面积是

1

2

×HF×EG=

1

2

×2×4=4，
故答案为：4．

点评：本题考查了矩形的性质，菱形的判定和性质，平行四边形的判定等知识点，关键是求出四边形EFGH是菱形．