题目内容
在△ABC和△DEF中,已知边AB=5,DE=5,AC=6,DF=8.三角形的内角∠A=50°,∠B=60°,∠D=40°,∠E=120°,若设△ABC的面积为S1,△DEF的面积为S2,则S1+S2等于
24
24
.分析:先根据∠A=50°,∠B=60°可求出∠C的度数,再AB=5,DE=5,∠A=50°,∠D=40°,∠E=120°可知,若把AB与DE重合则△CAF恰好构成直角三角形,再利用三角形的面积公式即可求解.
解答: 解:∵△ABC中,∠BAC=50°,∠ABC=60°,
解:∵△ABC中,∠BAC=50°,∠ABC=60°,
∴∠C=180°-∠BAC-∠ABC=180°-50°-60°=70°,
∵AB=5,DE=5,∠BAC=50°,∠EDF=40°,∠DEF=120°,
∴若把AB与DE重合则△CAF恰好构成直角三角形(如图所示),
∴s1+s2=s△CAF=
AC•DF=
×6×8=24.
故答案为:24.
 解:∵△ABC中,∠BAC=50°,∠ABC=60°,
解:∵△ABC中,∠BAC=50°,∠ABC=60°,∴∠C=180°-∠BAC-∠ABC=180°-50°-60°=70°,
∵AB=5,DE=5,∠BAC=50°,∠EDF=40°,∠DEF=120°,
∴若把AB与DE重合则△CAF恰好构成直角三角形(如图所示),
∴s1+s2=s△CAF=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:24.
点评:本题考查的是图形的剪拼,用到的知识点是三角形的面积及三角形内角和定理,解答此题时不要盲目求解,要注意观察两三角形的特点,能根据两三角形的边长及各角的度数,判断出若把AC与DE重合,则△ABF恰好构成直角三角形是解答此题的关键.

练习册系列答案
相关题目
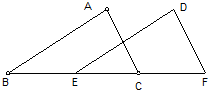 20、如图,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有四个条件,请你在其中选3个作为条件,余下的1个作为结论,使其成为一个真命题,并加以证明.
20、如图,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有四个条件,请你在其中选3个作为条件,余下的1个作为结论,使其成为一个真命题,并加以证明. 如图所示,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有六个条件,请你在其中选三个作为已知条件,余下的选一个作为结论,编写出一个真命题,并说明理由.①AB=DE;②AC=DF;③∠ABC=∠DEF;④BE=CF;⑤∠ACB=∠DEF;⑥∠A=∠D(填写序号即可)
如图所示,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有六个条件,请你在其中选三个作为已知条件,余下的选一个作为结论,编写出一个真命题,并说明理由.①AB=DE;②AC=DF;③∠ABC=∠DEF;④BE=CF;⑤∠ACB=∠DEF;⑥∠A=∠D(填写序号即可) 如图,已知BC∥EF,且BC=EF,AF=CD,则AB=DE,说明理由.
如图,已知BC∥EF,且BC=EF,AF=CD,则AB=DE,说明理由.