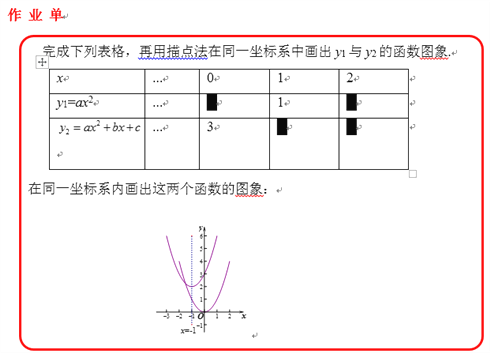
题目内容
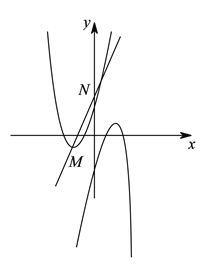
【题目】如图,在平面直角坐标系中,已知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,先将抛物线
,先将抛物线![]() 沿
沿![]() 轴翻折,再向右平移
轴翻折,再向右平移![]() 个单位长度后得到抛物线
个单位长度后得到抛物线![]() 直线
直线![]() 经过
经过![]() ,
, ![]() 两点.
两点.
(![]() )结合图象,直接写出不等式
)结合图象,直接写出不等式![]() 的解集.
的解集.
(![]() )若抛物线
)若抛物线![]() 的顶点与点
的顶点与点![]() 关于原点对称,求
关于原点对称,求![]() 的值及抛物线
的值及抛物线![]() 的解析式.
的解析式.
(![]() )若直线
)若直线![]() 沿
沿![]() 轴向右平移
轴向右平移![]() 个单位长度后,与(
个单位长度后,与(![]() )中的抛物线
)中的抛物线![]() 存在公共点,求代数式
存在公共点,求代数式![]() 的最大值.
的最大值.
【答案】(![]() )
)![]() .(
.( ![]() )
)![]() ;
; ![]() .(
.(![]() )
)![]() .
.
【解析】试题分析:(1)令抛物线C1的解析式中x=0,求出y值即可得出点N的坐标,再利用配方法将抛物线C1的解析式配方,即可得出顶点M的坐标,结合函数图象的上下位置关系,即可得出不等式的解集;(2)找出点M关于x轴对称的对称点的坐标,找出点M关于原点对称的对称点的坐标,二者横坐标做差即可得出p的值,根据抛物线的开口大小没变,开口方向改变,再结合平移后的抛物线的顶点坐标即可得出抛物线C2的解析式;(3)由点M、N的坐标利用待定系数法即可求出直线l的解析式,根据直线l沿y轴向下平移q个单位长度后与抛物线C2存在公共点,即可得出方程![]() 有实数根,利用根的判别式△≥0,即可求出q的取值范围,再根据一次函数的性质即可得出当
有实数根,利用根的判别式△≥0,即可求出q的取值范围,再根据一次函数的性质即可得出当![]() 时,
时, ![]() 取最大值,代入数据求出最值即可.
取最大值,代入数据求出最值即可.
试题解析:(![]() )由
)由![]() .
.
配成顶点式得![]() .
.
∴![]() ;
; ![]() .
.
则由图知, ![]() 的解集为
的解集为![]() .
.
(![]() )
)![]() ;
; ![]() .
.
(2)∵抛物线![]() 的顶点为M(2,1),
的顶点为M(2,1),
沿x轴翻折后的对称点坐标为(2,1).
∵抛物线C2的顶点与点M关于原点对称,
∴抛物线C2的顶点坐标为(2,-1),,
∴p=2(2)=4.
抛物线C2与C1开口大小相同,开口方向相反,
∴抛物线C2的解析式为![]() ..
..
(![]() )将
)将![]() ,
, ![]() 坐标代入
坐标代入![]() .
.
得![]() .
.
则平移后解析式为![]() .
.
又∵与![]() 有支点.
有支点.
即![]() 式中
式中![]() .
.
![]() .
.
得![]() .
.
代数式![]() .
.
![]() .
.
∴上式最大值为![]() ,上式
,上式![]() .
.

练习册系列答案
相关题目