题目内容
(1)
(2)(
+2)(
-2)
(3)已知
x=1+2x,求x2-4x-3的值.
| ||||
-
|
(2)(
| a |
| a |
(3)已知
| 5 |
分析:(1)根据多项式除以单项式法则展开,求出即可;
(2)根据平方差公式求出即可;
(3)求出x的值,再代入求出即可.
(2)根据平方差公式求出即可;
(3)求出x的值,再代入求出即可.
解答:解:(1)原式=
÷(-
)+
÷(-
)
=-
-
;
(2)原式=(
)2-22
=a-4;
(3)∵
x=1+2x,
∴x=
=
+2,
∴x2-4x-3
=x2-4x+4-7
=(x-2)2-7
=(
+2-2)2-7
=5-7
=-2.
| 18 |
| 3 |
| 6 |
| 3 |
=-
| 6 |
| 2 |
(2)原式=(
| a |
=a-4;
(3)∵
| 5 |
∴x=
| 1 | ||
|
| 5 |
∴x2-4x-3
=x2-4x+4-7
=(x-2)2-7
=(
| 5 |
=5-7
=-2.
点评:本题考查了二次根式的混合运算,平方差公式,完全平方公式的应用,主要考查学生的计算能力.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
计算2-3的结果是( )
| A、-6 | ||
| B、-8 | ||
C、-
| ||
D、
|
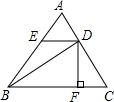 如图,在△ABC中,AC=15,BC=18,cosC=
如图,在△ABC中,AC=15,BC=18,cosC=| 3 |
| 5 |
| A、7.5 | B、9 | C、10 | D、5 |