题目内容
10.已知抛物线y=a(x+m)2经过点(2,-2),且对称轴是过点(3,0)且平行于y轴的直线.(1)求此函数的解析式;
(2)若把此抛物线绕顶点旋转180°得到的抛物线是什么?
分析 (1)由已知条件得出m=-3,然后把(2,-2)代入解析式即可求得a的值;
(2)把此抛物线绕顶点旋转180°得到的抛物线形状、大小相同,开口向上,据此即可求得解析式.
解答 解:(1)∵抛物线y=a(x+m)2的对称轴是过点(3,0)且平行于y轴的直线.
∴m=-3,
把(2,-2)代入得,-2=a(2-3)2,
解得a=-2,
∴此函数的解析式为y=-2(x-3)2;
(2)把此抛物线绕顶点旋转180°得到的抛物线形状、大小相同,开口向上,
所以旋转后的抛物线为y=2(x-3)2.
点评 本题考查了待定系数法求二次函数的解析式,熟练掌握待定系数法和二次函数的性质是解题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
2.下列说法正确的是( )
| A. | 0是最小的整数 | B. | 若|a|=|b|,则a=b | ||
| C. | 互为相反数的两数之和为零 | D. | 两个有理数,大的离原点远 |
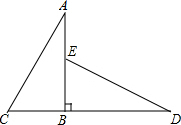 如图,已知AB⊥CD,垂足为B,AB=DB,AC=DE.请你判断∠D与∠A的关系,并说明理由.
如图,已知AB⊥CD,垂足为B,AB=DB,AC=DE.请你判断∠D与∠A的关系,并说明理由.