题目内容
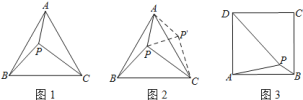
【题目】![]() 如图
如图![]() ,线段
,线段![]() ,
,![]() ,点
,点![]() 从点
从点![]() 开始绕着点
开始绕着点![]() 以
以![]() 的速度顺时针旋转一周回到点
的速度顺时针旋转一周回到点![]() 后停止,点
后停止,点![]() 同时出发沿射线
同时出发沿射线![]() 自
自![]() 点向
点向![]() 点运动,若点
点运动,若点![]() 、
、![]() 两点能恰好相遇,则点
两点能恰好相遇,则点![]() 运动的速度为________
运动的速度为________![]() ;
;

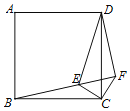
![]() 将一副三角板中的两块直角三角尺的直角顶点
将一副三角板中的两块直角三角尺的直角顶点![]() 按如图方式叠放在一起(其中,
按如图方式叠放在一起(其中,![]() ,
,![]() ,
,![]() ;
;![]() ).将三角尺
).将三角尺![]() 固定,另一三角尺
固定,另一三角尺![]() 的
的![]() 边从
边从![]() 边开始绕点
边开始绕点![]() 转动,转动速度与
转动,转动速度与![]() 问中
问中![]() 点速度相同,当
点速度相同,当![]() 且点
且点![]() 在直线
在直线![]() 的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出
的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出![]() 有可能的值及对应转动的时间;若不存在,请说明理由.
有可能的值及对应转动的时间;若不存在,请说明理由.
【答案】(1)![]() 或
或![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)求出点P到达点G和回到点M的时间,再根据点P、Q相遇的地点只有G、M,利用速度=路程÷时间列式计算即可得解;
(2)根据平行线的性质,按照旋转角从小到大的顺序依次确定出有两边平行时的旋转角,再求出时间即可.
解:(1)∵点P在⊙O上绕点O旋转的速度为15°/s,
∴点P到达点G的时间为180°÷15°=12s,
回到点M的时间为360°÷15°=24s,
∵点Q在射线NM上运动,
∴点P、Q相遇的地点只有G、M,
∴点Q运动的速度为(30-3×2)÷12=2cm/s,
或30÷24=1.25cm/s,
故答案为:![]() 或
或![]() ;
;
![]() 存在,
存在,
当![]() 时,
时,![]() ,用时
,用时![]() ,
,
当![]() 时,
时,![]() ,用时
,用时![]() ,
,
当![]() 时,
时,![]() ,用时
,用时![]() ,
,
当![]() 时,
时,![]() ,用时
,用时![]() ,
,
当![]() 时,
时,![]() ,用时
,用时![]() .
.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
【题目】九年级(1)班全班50名同学组成五个不同的兴趣爱好小组,每人都参加且只能参加一个小组,统计(不完全)人数如下表:
编号 | 一 | 二 | 三 | 四 | 五 |
人数 |
| 15 | 20 | 10 |
|
已知前面两个小组的人数之比是![]() .
.
解答下列问题:
(1)![]() .
.
(2)补全条形统计图:
(3)若从第一组和第五组中任选两名同学,求这两名同学是同一组的概率.(用树状图或列表把所有可能都列出来)