题目内容
【题目】阅读下面材料:
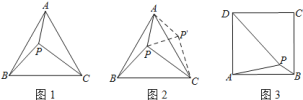
小伟遇到这样一个问题:如图![]() ,在正三角形
,在正三角形![]() 内有一点
内有一点![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.小伟是这样思考的:如图
的度数.小伟是这样思考的:如图![]() ,利用旋转和全等的知识构造
,利用旋转和全等的知识构造![]() ,连接
,连接![]() ,得到两个特殊的三角形,从而将问题解决.
,得到两个特殊的三角形,从而将问题解决.
(1)请你回答:图![]() 中
中![]() 的度数等于________.
的度数等于________.
参考小伟同学思考问题的方法,解决下列问题:
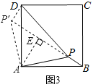
(2)如图![]() ,在正方形
,在正方形![]() 内有一点
内有一点![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数和正方形的边长.
的度数和正方形的边长.
【答案】150°
【解析】
把△APB绕点A逆时针旋转60°得到△![]() ,根据旋转的性质可得P
,根据旋转的性质可得P![]() A=PA,P
A=PA,P![]() C=PB,∠PAP
C=PB,∠PAP![]() =60°,再用勾股定理得出∠P
=60°,再用勾股定理得出∠P![]() PC=90°,然后求出∠AP
PC=90°,然后求出∠AP![]() C,即为∠APB的度数;把
C,即为∠APB的度数;把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,由旋转的性质,
,由旋转的性质,![]() ,
,![]() ,
,![]() ,然后判断出△APP
,然后判断出△APP![]() 是等腰三角形,根据等腰三角形性质求出PP
是等腰三角形,根据等腰三角形性质求出PP![]() ,∠PAP
,∠PAP![]() =45°,再运用勾股定理逆定理得出∠PP
=45°,再运用勾股定理逆定理得出∠PP![]() D=90°,然后求∠AP
D=90°,然后求∠AP![]() D,即为∠APB度数,在求出P
D,即为∠APB度数,在求出P![]() ,P,B三点共线,过点A作AE⊥PP
,P,B三点共线,过点A作AE⊥PP![]() 于E,根据等腰三角的性质求出AE,然后求BE,在直角三角形ABE中,利用勾股定理求出AB即可.
于E,根据等腰三角的性质求出AE,然后求BE,在直角三角形ABE中,利用勾股定理求出AB即可.
(1)![]() .
.
![]() 如图
如图![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,
由旋转的性质,![]() ,
,![]() ,
,![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
故![]() ,
,
∵![]() ,
,
∴点![]() 、
、![]() 、
、![]() 三点共线,
三点共线,
过点![]() 作
作![]() 于
于![]() ,
,
则![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() .
.

练习册系列答案
相关题目
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?