Question

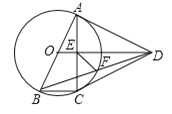
【题目】如图，平行四边形ABCD的周长为28，对角线AC、BD相交于点O，点E是CD的中点，BD=12，则△DOE的周长为(　　)

A.28B.12C.13D.17

Answer 1

【答案】C

【解析】

根据平行四边形的对边相等和对角线互相平分可得，OB=OD，BC+CD=14．又因为E点是CD的中点，可得OE是△BCD的中位线，可得DECD，OEBC，所以易求△DOE的周长．

解：∵ABCD的周长为28，

∴2(BC+CD)=28，则BC+CD=14．

∵四边形ABCD是平行四边形，对角线AC，BD相交于点O，BD=12，

∴OD=OBBD=6．

又∵点E是CD的中点，

∴OE是△BCD的中位线，DECD，

∴OEBC，

∴△DOE的周长=OD+OE+DEBD(BC+CD)=6+7=13，

即△DOE的周长为13．

故选：C．