题目内容
如图，弦AE∥直径CD，连AO，∠AOC=40゜，则
所对的圆心角的度数为
- A.40゜
- B.50゜
- C.60゜
- D.30゜
A
分析：首先根据弦AE∥直径CD，=
，再根据在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等可直接得到∠AOC=∠EOD=40°．
解答：
解：连接EO，
∵弦AE∥直径CD，
∴=，
∴∠AOC=∠EOD=40°，
故选：A．
点评：此题主要考查了圆心角、弧、弦的关系，关键是掌握在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．
分析：首先根据弦AE∥直径CD，
=，再根据在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等可直接得到∠AOC=∠EOD=40°．解答：
解：连接EO，∵弦AE∥直径CD，
∴
=，∴∠AOC=∠EOD=40°，
故选：A．
点评：此题主要考查了圆心角、弧、弦的关系，关键是掌握在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．
练习册系列答案
相关题目
25、如图，AB为⊙O直径，过弦AC的点C作CF⊥AB于点D，交AE所在直线于点F．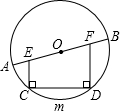
E，DF⊥CD交AB于F，
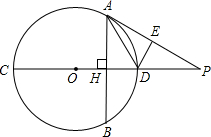如图，弦AB交圆O的直径CD于点H，且AH=BH，作△AHD关于直线AD的轴对称△AED，延长AE交CD的延长线于点P．
如图，弦AE∥直径CD，连AO，∠AOC=40゜，则