题目内容
 25、如图,AB为⊙O直径,过弦AC的点C作CF⊥AB于点D,交AE所在直线于点F.
25、如图,AB为⊙O直径,过弦AC的点C作CF⊥AB于点D,交AE所在直线于点F.(1)求证:AC2=AE•AF.
分析:要证明AC2=AE•AF,先把乘积的形式转化为比例的形式,然后看看在哪两个三角形中,看是不是能通过证明三角形的相似来证明.
解答: 证明:延长CF交⊙O于G,连接AG、EG,
证明:延长CF交⊙O于G,连接AG、EG,
∵CF⊥AB于点D,AB为⊙O直径,
∴AC=AG,∠C=∠AGC.
∵∠E=∠C,
∴∠AGC=∠E.
∵∠GAF=∠EAG,
∴△GAF∽△EAG.
∴AG:AE=AF:AG,AC:AE=AF:AC.
∴AC2=AE•AF.
 证明:延长CF交⊙O于G,连接AG、EG,
证明:延长CF交⊙O于G,连接AG、EG,∵CF⊥AB于点D,AB为⊙O直径,
∴AC=AG,∠C=∠AGC.
∵∠E=∠C,
∴∠AGC=∠E.
∵∠GAF=∠EAG,
∴△GAF∽△EAG.
∴AG:AE=AF:AG,AC:AE=AF:AC.
∴AC2=AE•AF.
点评:乘积的形式通常可以转化为比例的形式,通过相似三角形的性质得出.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 6、如图,AB为直径,∠BED=40°,则∠ACD=( )
6、如图,AB为直径,∠BED=40°,则∠ACD=( )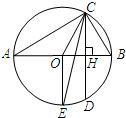 如图,AB为⊙O直径,CD为弦,且CD⊥AB,垂足为H.
如图,AB为⊙O直径,CD为弦,且CD⊥AB,垂足为H.
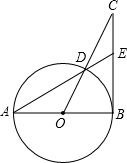 如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=25°,求∠A的度数.
如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=25°,求∠A的度数. 如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=20°,求∠A的度数.
如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=20°,求∠A的度数. 如图,AB为⊙O直径,BC与半径OD垂直于点C,∠B=28°,则∠A的度数为
如图,AB为⊙O直径,BC与半径OD垂直于点C,∠B=28°,则∠A的度数为