题目内容
14.设x1,x2是方程x2-x-2017=0的两个实数根,则x13+2018x2-2017=( )| A. | 2016 | B. | 2017 | C. | 2018 | D. | 2019 |
分析 先根据一元二次方程的解的定义得到x12=x1+2017,再计算x13=x12+2017x1=2018x1+2017,则原式可化简为2018(x1+x2),然后利用根与系数的关系求解.
解答 解:∵x1是方程x2-x-2017=0的两实数根,
∴x12=x1+2017,
∴x13=x12+2017x1=x1+2017+2017x1=2018x1+2017,
∴原式=2018x1+2017+2018x2-2017=2018(x1+x2),
∵x1,x2是方程x2-x-2017=0的两实数根,
∴x1+x2=1,
∴原式=2018.
故选C.
点评 本题主要考查了根与系数的关系,根据已知将原式化简,利用根与系数的关系是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4. 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中不一定成立的是( )
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中不一定成立的是( )
 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中不一定成立的是( )
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中不一定成立的是( )| A. | S△BEC=2S△CEF | B. | EF=CF | C. | ∠DCF=$\frac{1}{2}$∠BCD | D. | ∠DFE=3∠AEF |
2.下列计算正确的是( )
| A. | a-1•a-3=a3 | B. | (a-2)2=a4 | C. | a2÷a-4=a-2 | D. | (-2a)3=-8a3 |
9.下列计算正确的是( )
| A. | a2•a3=a6 | B. | a3÷a3=a | C. | 3a+3b=3ab | D. | (a3)2=a6 |
19.单项式xmy3与4x2yn的和是单项式,则nm的值是( )
| A. | 3 | B. | 6 | C. | 8 | D. | 9 |
6.正六边形的每个内角为( )
| A. | 120° | B. | 135° | C. | 140° | D. | 144° |
3.下列各数属于用科学记数法表示的是( )
| A. | 41.5×105 | B. | 0.413×104 | C. | -12×104 | D. | -7.16×105 |
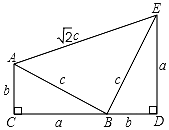 如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=$\sqrt{2}$c,这时我们把关于x的形如ax2+$\sqrt{2}$cx+b=0的一元二次方程称为“勾系一元二次方程”.
如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=$\sqrt{2}$c,这时我们把关于x的形如ax2+$\sqrt{2}$cx+b=0的一元二次方程称为“勾系一元二次方程”.