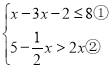题目内容
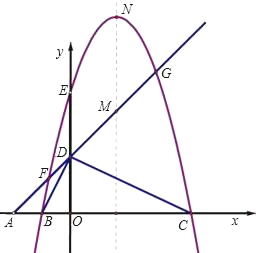
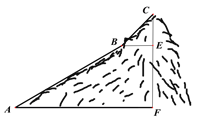
【题目】如图,正方形ABCD是一块绿化带,阴影部分EOFB,GHMN都是正方形的花圃,其中EOFB的顶点O是正方形中心.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】设正方形ABCD的边长为a,根据正方形的性质∠ACB=∠ACD=45°,AC=![]() a,再利用四边形BEOF为正方形易得CF=OF=BF=
a,再利用四边形BEOF为正方形易得CF=OF=BF=![]() a,则S正方形BEOF=
a,则S正方形BEOF=![]() a2,设正方形MNGH的边长为x,易得CM=AN=MN=x,即3x=
a2,设正方形MNGH的边长为x,易得CM=AN=MN=x,即3x=![]() a,解得x=
a,解得x=![]() a,则S正方形MNGH=
a,则S正方形MNGH=![]() a2,然后根据几何概率的意义,用两个小正方形的面积和除以正方形ABCD的面积即可得到小鸟落在花圃上的概率,从而得到小鸟不落在花圃上的概率.
a2,然后根据几何概率的意义,用两个小正方形的面积和除以正方形ABCD的面积即可得到小鸟落在花圃上的概率,从而得到小鸟不落在花圃上的概率.
设正方形ABCD的边长为a,
∵四边形ABCD为正方形,
∴∠ACB=∠ACD=45°,AC=![]() a,
a,
∵四边形BEOF为正方形,
∴CF=OF=BF,
∴S正方形BEOF=(![]() a)2=
a)2=![]() a2,
a2,
设正方形MNGH的边长为x,
∵△ANG和△CMH都是等腰直角三角形,
∴CM=AN=MN=x,
∴3x=![]() a,解得x=
a,解得x=![]() a,
a,
∴S正方形MNGH=(![]() a)2=
a)2=![]() a2,
a2,
∴小鸟不落在花圃上的概率=(![]() a2+
a2+![]() a2 )÷a2=
a2 )÷a2=![]() .
.
故选C.

 阅读快车系列答案
阅读快车系列答案【题目】某中学为了科学建设“学生健康成长工程”.随机抽取了部分学生家庭对其家长进行了主题为“周末孩子在家您关心吗?”的问卷调查,将回收的问卷进行分析整理,得到了如下的样本统计表和扇形统计图:
代号 | 情况分类 | 家庭数 |
| 带孩子玩并且关心其作业完成情况 | 16 |
| 只关心其作业完成情况 | b |
| 只带孩子玩 | 8 |
| 既不带孩子玩也不关心其作业完成情况 | d |
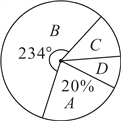
(1)求![]() 的值;
的值;
(2)该校学生家庭总数为500,学校决定按比例在![]() 类家庭中抽取家长组成培训班,其比例为
类家庭中抽取家长组成培训班,其比例为![]() 类取20%,
类取20%,![]() 类各取60%,请你估计该培训班的家庭数;
类各取60%,请你估计该培训班的家庭数;
(3)若在![]() 类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在
类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在![]() 类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.
类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.