题目内容
13.等腰三角形ABC的腰长为5,面积为$\frac{15}{2}$,则底角的正切值为4.分析 过点C作CH⊥AB于H,如图.根据条件可求出CH,在Rt△AHC中运用勾股定理可求出AH,从而得到BH,然后在Rt△BHC中运用三角函数的定义即可解决问题.
解答 解:过点C作CH⊥AB于H,如图.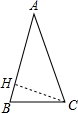
由题可得AB=AC=5,S△ABC=$\frac{15}{2}$.
则有$\frac{1}{2}$×5CH=$\frac{15}{2}$,
解得CH=3.
在Rt△AHC中,AH=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴BH=AB-AH=1,
在Rt△BHC中,tanB=$\frac{HC}{BH}$=4,
则底角的正切值为4.
故答案为4.
点评 本题主要考查了等腰三角形的性质、三角形的面积公式、勾股定理、三角函数的定义等知识,作一腰上的高是解决本题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
3.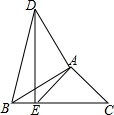 如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )
如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )
 如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )
如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
4.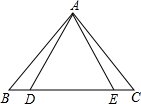 如图,已知△ABE≌△ACD,下列不正确的等式是( )
如图,已知△ABE≌△ACD,下列不正确的等式是( )
 如图,已知△ABE≌△ACD,下列不正确的等式是( )
如图,已知△ABE≌△ACD,下列不正确的等式是( )| A. | AB=AC | B. | ∠BAE=∠CAD | C. | BE=DC | D. | AD=DE |
18.正八边形的每个内角的度数是( )
| A. | 144° | B. | 140° | C. | 135° | D. | 120° |
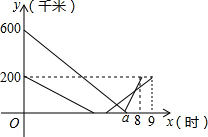 甲、乙两车在连通A、B、C三地的公路上行驶,B地在A地、C地之间,甲车从A地出发匀速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地并在B地停留1h后,按原路原速返回到C地.在两车行驶的过程中,甲、乙两车距B地的路程y(km)与行驶时间x(h)之间的函数图象如图所示.下列说法:
甲、乙两车在连通A、B、C三地的公路上行驶,B地在A地、C地之间,甲车从A地出发匀速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地并在B地停留1h后,按原路原速返回到C地.在两车行驶的过程中,甲、乙两车距B地的路程y(km)与行驶时间x(h)之间的函数图象如图所示.下列说法: